
HL Paper 2
The concentration of a solution of a weak acid, such as ethanedioic acid, can be determined
by titration with a standard solution of sodium hydroxide, NaOH (aq).
5.00 g of an impure sample of hydrated ethanedioic acid, (COOH)2•2H2O, was dissolved in water to make 1.00 dm3 of solution. 25.0 cm3 samples of this solution were titrated against a 0.100 mol dm-3 solution of sodium hydroxide using a suitable indicator.
(COOH)2 (aq) + 2NaOH (aq) → (COONa)2 (aq) + 2H2O (l)
The mean value of the titre was 14.0 cm3.
(i) Suggest a suitable indicator for this titration. Use section 22 of the data booklet.
(ii) Calculate the amount, in mol, of NaOH in 14.0 cm3 of 0.100 mol dm-3 solution.
(iii) Calculate the amount, in mol, of ethanedioic acid in each 25.0 cm3 sample.
(iv) Determine the percentage purity of the hydrated ethanedioic acid sample.
Draw the Lewis (electron dot) structure of the ethanedioate ion, –OOCCOO–.
Outline why all the C–O bond lengths in the ethanedioate ion are the same length and suggest a value for them. Use section 10 of the data booklet.
Explain how ethanedioate ions act as ligands.
Markscheme
i
phenolphthalein
OR
phenol red
ii
«n(NaOH) = \(\left( {\frac{{14.0}}{{1000}}} \right)\) dm3 × 0.100 mol dm-3 =» 1.40 × 10-3 «mol»
iii
«\(\frac{1}{2}\) × 1.40 × 10-3 =» 7.00 × 10-4 «mol»
iv
ALTERNATIVE 1:
«mass of pure hydrated ethanedioic acid in each titration = 7.00 × 10-4 mol × 126.08 g mol-1 =» 0.0883 / 8.83 × 10-2 «g»
mass of sample in each titration = «\(\frac{{25}}{{1000}}\) × 5.00 g =» 0.125 «g»
«% purity = \(\frac{{0.0883{\rm{g}}}}{{0.125{\rm{g}}}}\) × 100 =» 70.6 «%»
ALTERNATIVE 2:
«mol of pure hydrated ethanedioic acid in 1 dm3 solution = 7.00 × 10-4 × \(\frac{{1000}}{{25}}\)=» 2.80 × 10-2 «mol»
«mass of pure hydrated ethanedioic acid in sample = 2.80 × 10-2 mol × 126.08 g mol-1 =» 3.53 «g»
«% purity = \(\frac{{3.53{\rm{g}}}}{{5.00{\rm{g}}}}\) × 100 =» 70.6 «%»
ALTERNATIVE 3:
mol of hydrated ethanedioic acid (assuming sample to be pure) = \(\frac{{5.00{\rm{g}}}}{{126.08{\rm{gmo}}{{\rm{l}}^{{\rm{ - 1}}}}}}\) = 0.03966 «mol»
actual amount of hydrated ethanedioic acid = «7.00 × 10-4 × \(\frac{{1000}}{{25}}\) =» 2.80 × 10-2 «mol»
«% purity = \(\frac{{2.80 \times {{10}^{ - 2}}}}{{0.03966}}\) × 100 =» 70.6 «%»
Award suitable part marks for alternative methods.
Award [3] for correct final answer.
Award [2 max] for 50.4 % if anhydrous ethanedioic acid assumed.
Accept single negative charges on two O atoms singly bonded to C.
Do not accept resonance structures.
Allow any combination of dots/crosses or lines to represent electron pairs.
electrons delocalized «across the O–C–O system»
OR
resonance occurs
Accept delocalized π-bond(s).
No ECF from (d).
122 «pm» < C–O < 143 «pm»
Accept any answer in range 123 «pm» to 142 «pm».
Accept “bond intermediate between single and double bond” or “bond order 1.5”.
coordinate/dative/covalent bond from O to «transition» metal «ion»
OR
acts as a Lewis base/nucleophile
can occupy two positions
OR
provide two electron pairs from different «O» atoms
OR
form two «coordinate/dative/covalent» bonds «with the metal ion»
OR
chelate «metal/ion»
Examiners report
Hydrazine, N2H4, is a valuable rocket fuel.
The equation for the reaction between hydrazine and oxygen is given below.
\[{{\text{N}}_2}{{\text{H}}_4}({\text{l)}} + {{\text{O}}_2}({\text{g)}} \to {{\text{N}}_2}({\text{g)}} + 2{{\text{H}}_2}{\text{O(l)}}\]
The reaction between \({{\text{N}}_2}{{\text{H}}_4}({\text{aq)}}\) and \({\text{HCl(aq)}}\) can be represented by the following equation.
\[{{\text{N}}_2}{{\text{H}}_4}({\text{aq)}} + 2{\text{HCl(aq)}} \to {{\text{N}}_2}{\text{H}}_6^{2 + }({\text{aq)}} + 2{\text{C}}{{\text{l}}^ - }({\text{aq)}}\]
(i) Draw the Lewis (electron dot) structure for N2H4 showing all valence electrons.
(ii) State and explain the H–N–H bond angle in hydrazine.
Hydrazine and ethene, C2H4, are hydrides of adjacent elements in the periodic table. The boiling point of hydrazine is much higher than that of ethene. Explain this difference in terms of the intermolecular forces in each compound.
(i) The enthalpy change of formation, \(\Delta H_{\text{f}}^\Theta \), of liquid hydrazine is \({\text{50.6 kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\). Use this value, together with data from Table 12 of the Data Booklet, to calculate the enthalpy change for this reaction.
(ii) Use the bond enthalpy values from Table 10 of the Data Booklet to determine the enthalpy change for this reaction.
(iii) Identify the calculation that produces the most accurate value for the enthalpy change for the reaction given and explain your choice.
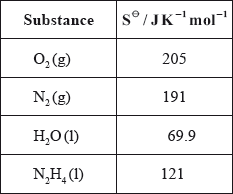
(iv) Calculate \(\Delta {S^\Theta }\) for the reaction using the data below and comment on its magnitude.
(v) Calculate \(\Delta {G^\Theta }\) for the reaction at 298 K.
(vi) Predict, giving a reason, the spontaneity of the reaction above at both high and low temperatures.
The reaction between \({{\text{N}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{(aq)}}\) and HCl(aq) can be represented by the following equation.
\[{{\text{N}}_2}{{\text{H}}_4}({\text{aq)}} + 2{\text{HCl(aq)}} \to {{\text{N}}_2}{\text{H}}_6^{2 + }({\text{aq)}} + 2{\text{C}}{{\text{l}}^ - }({\text{aq)}}\]
(i) Identify the type of reaction that occurs.
(ii) Predict the value of the H–N–H bond angle in \({{\text{N}}_{\text{2}}}{\text{H}}_{\text{6}}^{{\text{2}} + }\).
(iii) Suggest the type of hybridization shown by the nitrogen atoms in \({{\text{N}}_{\text{2}}}{\text{H}}_{\text{6}}^{{\text{2}} + }\).
Markscheme
(i) 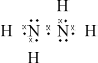 ;
;
Accept x’s, dots or lines for electron pairs
(ii) H–N–H \( < \) 109 / any angle between 104° and 109°;
due to four centres of electron charge / four electron pairs (one of which is a lone \({{\text{e}}^ - }\) pair);
extra repulsion due to lone electron pairs;
Do not allow ECF for wrong Lewis structures.
weaker van der Waals’/London/dispersion/intermolecular forces in ethene;
stronger (intermolecular) hydrogen bonding in hydrazine;
If no comparison between strengths then [1 max].
(i) \(\Delta H_{\text{r}}^\Theta = \Sigma \Delta H_{\text{f}}^\Theta {\text{ products}} - \Sigma \Delta H_{\text{f}}^\Theta {\text{ reactants}}\);
Can be implied by working.
\(\Delta H_{\text{f}}^\Theta {\text{(}}{{\text{H}}_2}{\text{O(l))}} = - 286{\text{ (kJ)}}\);
\(\Delta H_{\text{r}}^\Theta = 2( - 286) - 50.6 = - 622.6{\text{ (kJ)}}\);
(ii) bonds broken: 4N–H, N–N, O=O / \( + {\text{2220 (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
bonds formed: N\(\equiv\)N, 4O-H / \( - 2801{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
\( - 581{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
Award [3] for correct final answer.
(iii) value based on \(\Delta {H_{\text{f}}}\) more accurate;
\(\Delta {H_{\text{f}}}\) accurate for compounds in reaction;
bond energy calculation assumes average bond energies;
(bond energy calculation) only applies to gaseous states / ignores intermolecular bonds;
(iv) \(\Delta {S^\Theta } = \Sigma {S^\Theta }{\text{ (products)}} - \Sigma {S^\Theta }{\text{ (reactants)}}\);
Can be implied by working.
\( = 191 + (2 \times 69.9) - 205 - 121 = + 4.8{\text{ (J}}\,{{\text{K}}^{ - 1}}{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
small value since number of mol of g on both sides the same;
(v) \(\Delta {G^\Theta } = - 622.6 - 298(0.0048)\);
\( = - 624.0{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
Allow 623.9 to 624.1.
(vi) all reactions are spontaneous;
\(\Delta G\) is negative (at high temperatures and low temperatures);
(i) acid-base/neutralization;
(ii) 109°/109.5°;
(iii) sp3;
No ECF if bond angle incorrect in (ii).
Examiners report
The Lewis structure for hydrazine proved to be difficult for some in (a). Incorrect answers had double bonds appearing between the two nitrogen atoms or lone pairs missing. Those who could draw the correct structure in (i) gave the correct bond angle, but the explanation was often incomplete. Few mentioned either the four electron domains around the central atom or the extra repulsion of the lone pair.
In part (b) most candidates knew that hydrogen bonding was present in hydrazine and Van der Waals‟ forces in ethene but failed to give a comparison of the relative strength of the intermolecular forces.
Some candidates struggled to calculate the enthalpy changes from enthalpy changes of formation in (c) (i) as they were unable to relate the enthalpy change of combustion of hydrogen to the enthalpy change of formation of water.
The bond energy and entropy calculations were more successful with many candidates benefitting from ECF from their incorrect Lewis structures in (a). It was encouraging to see many correct unit conversions for the calculation of \(\Delta G\). A number of candidates incorrectly described the combination of hydrazine and hydrochloric acid as a redox reaction, but many were able to identify the bond angle and hybridization in \({{\text{N}}_{\text{2}}}{\text{H}}_{\text{6}}^{{\text{2}} + }\).
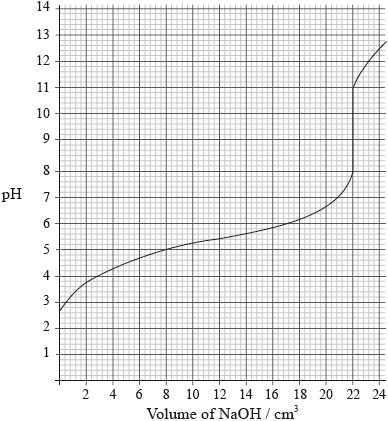
A \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) solution of a weak monoprotic acid, HA(aq), is titrated with \({\text{0.155 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide, NaOH(aq), and the following graph is obtained.
0.100 mol of ammonia, \({\text{N}}{{\text{H}}_{\text{3}}}\), was dissolved in water to make \({\text{1.00 d}}{{\text{m}}^{\text{3}}}\) of solution. This solution has a hydroxide ion concentration of \({\text{1.28}} \times {\text{1}}{{\text{0}}^{ - 3}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\).
Determine the pH at the equivalence point.
Explain, using an equation, why the equivalence point is not at \({\text{pH}} = 7\).
Calculate the concentration of the weak acid before the addition of any NaOH(aq).
Estimate, using data from the graph, the dissociation constant, \({K_{\text{a}}}\), of the weak acid, HA, showing your working.
Suggest an appropriate indicator for this titration.
Describe qualitatively the action of an acid-base indicator.
Explain what is meant by the term buffer solution.
Calculate the pH of a solution prepared by mixing \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.200 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ C}}{{\text{H}}_{\text{3}}}{\text{COOH(aq)}}\) and \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of ,\({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ NaOH(aq)}}\) showing your working.
Determine the pH of the solution.
Calculate the base dissociation constant, \({K_{\text{b}}}\), for ammonia.
Markscheme
9.5;
Accept any value in the range 9.4–9.6.
titration involves a weak acid and a strong base;
salt formed at equivalence point is basic due to hydrolysis;
\({{\text{A}}^ - }{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{HA(aq)}} + {\text{O}}{{\text{H}}^ - }{\text{(aq)}}\);
Ignore state symbols.
\(\frac{{{\text{0.155}} \times {\text{22.0}} \times {\text{1}}}}{{{\text{25.0}} \times {\text{1}}}}\);
\( = {\text{0.136 (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
at half neutralization point, \({\text{pH}} = {\text{p}}{K_{\text{a}}}\);
\({\text{p}}{K_{\text{a}}} = {\text{5.3}}\);
Accept any value in the range 5.2–5.4.
\({K_{\text{a}}} = {\text{5.0}} \times {\text{1}}{{\text{0}}^{ - 6}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
Accept calculations based on initial pH or on pH of salt.
phenolphthalein;
Accept thymolphthalein.
Allow ECF from (a)(i).
\({\text{HIn(aq)}} \rightleftharpoons {{\text{H}}^ + }{\text{(aq)}} + {\text{I}}{{\text{n}}^ - }{\text{(aq)}}\);
colour A colour B
in presence of acid/\({{\text{H}}^ + }\), equilibrium shifts to left, colour A;
in presence of base/\({\text{O}}{{\text{H}}^ - }{\text{ }}\), equilibrium shifts to right, colour B;
buffer solution resists change in pH;
on addition of small amount of acid or base;
after mixing \({\text{[C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ - }{\text{]}} = {\text{[C}}{{\text{H}}_3}{\text{COOH]}} = {\text{0.050 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\);
\({K_{\text{a}}} = {\text{[}}{{\text{H}}^ + }{\text{]/p}}{K_{\text{a}}} = {\text{pH}}\);
\({\text{pH}} = {\text{4.76}}\);
Working must be shown to score [3].
Award [1] if 4.76 stated with no working.
\({\text{[}}{{\text{H}}^ + }{\text{]}} = \frac{{{\text{1.00}} \times {\text{1}}{{\text{0}}^{ - 14}}}}{{{\text{1.28}} \times {\text{1}}{{\text{0}}^{ - 3}}}} = {\text{7.81}} \times {\text{1}}{{\text{0}}^{ - 12}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}/{\text{pOH}} = - \log 1.28 \times {10^{ - 3}} = 2.90\);
\({\text{pH}} = (14.0 - 2.90) = 11.1\);
Award [2] for the correct final answer
\({K_{\text{b}}} = \frac{{{\text{[NH}}_4^ + {\text{][O}}{{\text{H}}^ - }{\text{]}}}}{{{\text{[N}}{{\text{H}}_3}{\text{]}}}}\);
\( = \frac{{{{(1.28 \times {{10}^{ - 3}})}^2}}}{{0.100{\text{ - }}0.00128}}/\frac{{{{(1.28 \times {{10}^{ - 3}})}^2}}}{{0.100}}\);
\( = 1.66 \times {10^{ - 5}}/1.64 \times {10^{ - 5}}\);
Examiners report
Most candidates were able to determine the pH at the equivalence point.
Salt hydrolysis was very poorly understood by many candidates and therefore they were not able to write an equation.
In part (b) most candidates described the use of indicators during titrations, but lost credit for not using the reversible equilibrium equation to explain how they function qualitatively.
Part c (ii) baffled the majority of candidates. It is surprising to see that calculations based on buffers are almost an exclusive domain of the better candidates.
In part (e), only the able candidates scored the maximum five marks for calculating the pH and the base dissociation constant for ammonia.
Overall knowledge of acid-base chemistry was considerably weak, especially calculations.
Hypochlorous acid, HOCl(aq), is an example of a weak acid.
A household bleach contains sodium hypochlorite, NaOCl(aq), at a concentration of \({\text{0.705 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\). The hypochlorite ion, \({\text{OC}}{{\text{l}}^ - }{\text{(aq)}}\) is a weak base.
\[{\text{OC}}{{\text{l}}^ - }{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{HOCl(aq)}} + {\text{O}}{{\text{H}}^ - }{\text{(aq)}}\]
State the expression for the ionic product constant of water, \({K_{\text{w}}}\).
The \({\text{p}}{K_{\text{a}}}\) value of HOCl(aq) is 7.52. Determine the \({K_{\text{b}}}\) value of \({\text{OC}}{{\text{l}}^ - }{\text{(aq)}}\) assuming a temperature of 298 K.
Determine the concentration of \({\text{O}}{{\text{H}}^ - }{\text{(aq)}}\), in \({\text{mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\), at equilibrium and state one assumption made in arriving at your answer other than a temperature of 298 K.
Calculate the pH of the bleach.
Markscheme
\({\text{(}}{K_{\text{w}}} = {\text{)[}}{{\text{H}}^ + }{\text{(aq)][O}}{{\text{H}}^ - }{\text{(aq)]}}\);
Do not penalize if (aq) not stated.
H3O+ may be given instead of H+.
Do not mark awarded if square brackets are omitted or are incorrect.
\({\text{(p}}{K_{\text{b}}} = (14.00 - 7.52 = ){\text{ }}6.48{\text{ and) }}{K_{\text{b}}} = ({10^{ - 6.48}}) = 3.3 \times {10^{ - 7}}\);
Do not award mark if answer just left as 10–6.48.
\({K_{\text{b}}} = \frac{{{\text{[HOCl][O}}{{\text{H}}^ - }{\text{]}}}}{{{\text{[OC}}{{\text{l}}^ - }{\text{]}}}} = \frac{{{x^2}}}{{0.705}} = 3.3 \times {10^{ - 7}}\);
\({\text{[O}}{{\text{H}}^ - }{\text{]}} = 4.8 \times {10^{ - 4}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
Award [2] for correct value of [OH–].
\({\text{OC}}{{\text{l}}^ - }\) only partially hydrolysed / x negligible (compared to \({\text{OC}}{{\text{l}}^ - }\)) / OWTTE;
Accept [HOCl] = [OH–].
\({\text{[}}{{\text{H}}_3}{{\text{O}}^ + }{\text{]}}/{\text{[}}{{\text{H}}^ + }{\text{]}} = \frac{{{K_{\text{w}}}}}{{{\text{[O}}{{\text{H}}^ - }{\text{]}}}} = \frac{{1.00 \times {{10}^{ - 14}}}}{{4.8 \times {{10}^{ - 4}}}} = 2.1 \times {10^{ - 11}}\);
\({\text{pH}} = \left( { - {{\log }_{10}}{\text{[}}{{\text{H}}_3}{{\text{O}}^ + }{\text{]}}/ - {{\log }_{10}}{\text{[}}{{\text{H}}^ + }{\text{]}} = - {{\log }_{10}}(2.1 \times {{10}^{ - 11}}) = } \right)10.68\);
Award [2] for correct final answer.
Examiners report
This was generally well answered.
Many of the better students scored full marks here, and even the weaker students gained some marks.
Many of the better students scored full marks here, and even the weaker students gained some marks.
Many of the better students scored full marks here, and even the weaker students gained some marks.
The Haber process enables the large-scale production of ammonia needed to make fertilizers.
The equation for the Haber process is given below.
\[{{\text{N}}_2}({\text{g)}} + 3{{\text{H}}_2}({\text{g)}} \rightleftharpoons {\text{2N}}{{\text{H}}_3}({\text{g)}}\]
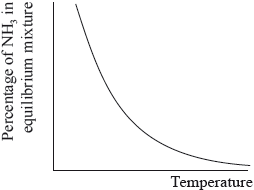
The percentage of ammonia in the equilibrium mixture varies with temperature.
Ammonia can be converted into nitric acid, \({\text{HN}}{{\text{O}}_{\text{3}}}{\text{(aq)}}\), and hydrocyanic acid, HCN(aq). The \({\text{p}}{K_{\text{a}}}\) of hydrocyanic acid is 9.21.
A student decided to investigate the reactions of the two acids with separate samples of \({\text{0.20 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide solution.
(i) Use the graph to deduce whether the forward reaction is exothermic or endothermic and explain your choice.
(ii) State and explain the effect of increasing the pressure on the yield of ammonia.
(iii) Deduce the equilibrium constant expression, \({K_{\text{c}}}\), for the reaction.
(iv) A mixture of 1.00 mol \({{\text{N}}_{\text{2}}}\) and 3.00 mol \({{\text{H}}_{\text{2}}}\) was placed in a \({\text{1.0 d}}{{\text{m}}^{\text{3}}}\) flask at 400 °C. When the system was allowed to reach equilibrium, the concentration of was found to be \({\text{0.062 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\). Determine the equilibrium constant, \({K_{\text{c}}}\), of the reaction at this temperature.
(v) Iron is used as a catalyst in the Haber process. State the effect of a catalyst on the value of \({K_{\text{c}}}\).
(i) Distinguish between the terms strong and weak acid and state the equations used to show the dissociation of each acid in aqueous solution.
(ii) Deduce the expression for the ionization constant, \({K_{\text{a}}}\), of hydrocyanic acid and calculate its value from the \({\text{p}}{K_{\text{a}}}\) value given.
(iii) Use your answer from part (b) (ii) to calculate the \({\text{[}}{{\text{H}}^ + }{\text{]}}\) and the pH of an aqueous solution of hydrocyanic acid of concentration \({\text{0.108 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\). State one assumption made in arriving at your answer.
A small piece of magnesium ribbon is added to solutions of nitric and hydrocyanic acid of the same concentration at the same temperature. Describe two observations that would allow you to distinguish between the two acids.
(i) Calculate the volume of the sodium hydroxide solution required to react exactly with a \({\text{15.0 c}}{{\text{m}}^{\text{3}}}\) solution of \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) nitric acid.
(ii) The following hypothesis was suggested by the student: “Since hydrocyanic acid is a weak acid it will react with a smaller volume of the \({\text{0.20 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide solution.” Comment on whether or not this is a valid hypothesis.
(iii) Use Table 16 of the Data Booklet to identify a suitable indicator for the titration of sodium hydroxide and hydrocyanic acid.
Markscheme
(i) exothermic;
Accept either of the following for the second mark.
increasing temperature favours endothermic/reverse reaction;
as yield decreases with increasing temperature;
(ii) yield increases / equilibrium moves to the right / more ammonia;
increase in pressure favours the reaction which has fewer moles of gaseous products;
(iii) \({K_{\text{c}}} = \frac{{{{{\text{[N}}{{\text{H}}_3}{\text{]}}}^2}}}{{{\text{[}}{{\text{N}}_2}{\text{][}}{{\text{H}}_2}{{\text{]}}^3}}}\);
(iv) \({\text{[}}{{\text{N}}_2}{\text{]}}\): (at equilibrium \( = 1.00 - 0.031 = \)) \({\text{0.969 (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({\text{[}}{{\text{H}}_2}{\text{]}}\): (at equilibrium \( = 3.00 - 3(0.031) = \)) \({\text{2.91 (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({K_{\text{c}}}{\text{ }}\left( { = \frac{{{{{\text{(0.062)}}}^2}}}{{{\text{(0.969) (2.91}}{{\text{)}}^3}}}} \right) = {\text{1.6(1)}} \times {\text{1}}{{\text{0}}^{ - 4}}\);
Ignore units.
Award [1] for Kc = 1.4 \( \times \) 10–4
(v) no effect;
(i) strong acid completely dissociated/ionized and weak acid partially dissociated/ionized;
\({\text{HN}}{{\text{O}}_3}{\text{(aq)}} \to {{\text{H}}^ + }{\text{(aq)}} + {\text{NO}}_3^ - {\text{(aq)}}\);
\({\text{HCN(aq)}} \rightleftharpoons {{\text{H}}^ + }{\text{(aq)}} + {\text{C}}{{\text{N}}^ - }{\text{(aq)}}\);
Insist on both arrows as shown.
State symbols not needed.
Accept H2O and H3O+.
(ii) \({K_{\text{a}}} = \frac{{{\text{[}}{{\text{H}}^ + }{\text{][C}}{{\text{N}}^ - }{\text{]}}}}{{{\text{[HCN]}}}}\);
Allow H3O+ instead of H+.
\({K_{\text{a}}} = {10^{ - 9.21}} = 6.17 \times {10^{ - 10}}\);
(iii) \({[{{\text{H}}^ + }] = \sqrt {{K_{\text{a}}}[{\text{HCN}}]} /\sqrt {(6.17 \times {{10}^{ - 10}} \times 0.108)} }\);
\({ = 8.16 \times {{10}^{ - 6}}}\);
Allow in the range 8.13 \( \times \) 10–6 to 8.16 \( \times \) 10–6.
\({\text{pH}} = 5.09\);
OR
\({{\text{pH}} = \frac{1}{2}{\text{(p}}{K_{\text{a}}} - {\text{log}}[{\text{HCN}}])/\frac{1}{2}(9.21 - \log \,0.108)}\);
\({ = 5.09}\);
\({\text{[}}{{\text{H}}^ + }{\text{]}} = {10^{ - 5.09}} = 8.16 \times {10^{ - 6}}\);
Allow in the range 8.13 \( \times \) 10–6 to 8.16 \( \times \) 10–6.
If expression for [H+] missing but both answers correct, award [3], if one answer
correct, award [2].
assume \({\text{[}}{{\text{H}}^ + }{\text{]}} \ll 0.108\) / negligible dissociation;
With HNO3:
faster rate of bubble/hydrogen/gas production;
faster rate of magnesium dissolving;
higher temperature change;
Accept opposite argument for HCN.
Reference to specific observations needed.
Award [1] if 2 observations given but acid is not identified.
(i) (nitric acid) 7.5 cm3;
(ii) not valid as hydrocyanic acid reacts with same volume/ 7.5 cm3;
(iii) bromothymol blue / phenol red / phenolphthalein;
Examiners report
Equilibrium is a topic that has shown substantial improvement in recent sessions with some very well produced arguments. The reaction was correctly described as exothermic with a reason correctly given in most cases. Most candidates knew that yield would increase with increased pressure, but some failed to identify the change in the number of “gaseous” molecules as the reason. More candidates had difficulty with the equilibrium constant calculation often using the initial not equilibrium concentrations.
In (b) most correctly defined strong and weak acids and many also wrote correct equations. A few, however, missed the equilibrium sign for hydrocyanic acid. HA, CH3COOH and HCl were commonly given instead of HCN and HNO3, suggesting that students sometimes have difficulty applying general concepts to specific cases. It was encouraging to see many candidates determine the pH from the pKa value including the assumption that there is negligible dissociation, as this has challenged students in previous sessions. A significant number of weaker candidates reported however that the acid solution would have pH values above 7.
Part (c) presented problems with many candidates unable to describe specific observations related to rate which would distinguish between a strong and weak acid and simply stated that the reaction would be faster.
The moles calculation was answered well in (d) with most candidates able to identify phenolphthalein as a suitable indicator.
Water is an important substance that is abundant on the Earth’s surface.
Buffer solutions resist small changes in pH. A phosphate buffer can be made by dissolving \({\text{Na}}{{\text{H}}_{\text{2}}}{\text{P}}{{\text{O}}_{\text{4}}}\) and \({\text{N}}{{\text{a}}_{\text{2}}}{\text{HP}}{{\text{O}}_{\text{4}}}\) in water, in which \({\text{Na}}{{\text{H}}_{\text{2}}}{\text{P}}{{\text{O}}_{\text{4}}}\) produces the acidic ion and \({\text{N}}{{\text{a}}_{\text{2}}}{\text{HP}}{{\text{O}}_{\text{4}}}\) produces the conjugate base ion.
A \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution is placed in a flask and titrated with a \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) hydrochloric acid solution.
(i) State the expression for the ionic product constant of water, \({K_{\text{w}}}\).
(ii) Explain why even a very acidic aqueous solution still has some \({\text{O}}{{\text{H}}^ - }\) ions present in it.
(iii) State and explain the effect of increasing temperature on the value of \({K_{\text{w}}}\) given that the ionization of water is an endothermic process.
(iv) State and explain the effect of increasing temperature on the pH of water.
(i) Deduce the acid and conjugate base ions that make up the phosphate buffer and state the ionic equation that represents the phosphate buffer.
(ii) Describe how the phosphate buffer minimizes the effect of the addition of a
strong base, \({\text{O}}{{\text{H}}^ - }{\text{(aq)}}\), to the buffer. Illustrate your answer with an ionic equation.
(iii) Describe how the phosphate buffer minimizes the effect of the addition of a
strong acid, \({{\text{H}}^ + }{\text{(aq)}}\), to the buffer. Illustrate your answer with an ionic equation.
(i) Explain why the pH of the ammonia solution is less than 13.
(ii) Estimate the pH at the equivalence point for the titration of hydrochloric acid with ammonia and explain your reasoning.
(iii) State the equation for the reaction of ammonia with water and write the \({K_{\text{b}}}\) expression for \({\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\).
(iv) When half the ammonia has been neutralized (the half-equivalence point), the pH of the solution is 9.25. Deduce the relationship between \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) and \({\text{[NH}}_4^ + {\text{]}}\) at the
half-equivalence point.
(v) Determine \({\text{p}}{K_{\text{b}}}\) and \({K_{\text{b}}}\) for ammonia based on the pH at the half-equivalence point.
(vi) Describe the significance of the half-equivalence point in terms of its effectiveness as a buffer.
Markscheme
(i) \({\text{(}}{K_{\text{w}}}{\text{)}} = {\text{[}}{{\text{H}}^ + }{\text{][O}}{{\text{H}}^ - }{\text{] / (}}{K_{\text{w}}}{\text{)}} = {\text{[}}{{\text{H}}_{\text{3}}}{{\text{O}}^ + }{\text{][O}}{{\text{H}}^ - }{\text{]}}\);
Do not award mark if [ ] omitted or other brackets are used.
(ii) \({\text{[}}{{\text{H}}^ + }{\text{]}}\) increases, \({\text{[O}}{{\text{H}}^ - }{\text{]}}\) decreases but still some present (\({K_{\text{w}}}\) constant) / \({\text{[O}}{{\text{H}}^ - }{\text{]}}\) cannot go to zero as equilibrium present / \({\text{[O}}{{\text{H}}^ - }{\text{]}} = \frac{{{K_{\text{w}}}}}{{{\text{[}}{{\text{H}}^ + }{\text{]}}}}\), thus \({\text{[O}}{{\text{H}}^ - }{\text{]}}\) cannot be zero / OWTTE;
Accept equilibrium present.
(iii) (changing T disturbs equilibrium) forward reaction favoured / equilibrium shifts to the right;
to use up (some of the) heat supplied;
\({{K_{\text{w}}}}\) increases (as both \({{\text{[}}{{\text{H}}^ + }{\text{]}}}\) and \({\text{[O}}{{\text{H}}^ - }{\text{]}}\) increase);
(iv) (as \({{\text{[}}{{\text{H}}^ + }{\text{]}}}\) increases) pH decreases / \({\text{pH}} < 7\);
No mark for more acidic.
inverse relationship between pH and \({\text{[}}{{\text{H}}^ + }{\text{] / pH}} = - \log {\text{[}}{{\text{H}}^ + }{\text{] / pH}} = {\log _{10}}\frac{{\text{1}}}{{{\text{[}}{{\text{H}}^ + }{\text{]}}}}\);
Accept [H3O+] in place of [H+].
(i) Acid: \({{\text{H}}_2}{\text{PO}}_4^ - \);
(Conjugate) base: \({\text{HPO}}_4^{2 - }\);
No mark for NaH2PO4 or Na2HPO4.
\({{\text{H}}_2}{\text{PO}}_4^ - {\text{(aq)}} \rightleftharpoons {{\text{H}}^ + }{\text{(aq)}} + {\text{HPO}}_4^{2 - }{\text{(aq)}}\);
Accept reverse equation or reaction with water.
Ignore state symbols, but equilibrium sign is required.
Accept OH– (ions) react with H+ (ions) to form H2O.
(ii) strong base/\({\text{O}}{{\text{H}}^ - }\) replaced by weak base (\({\text{HPO}}_4^{2 - }\), and effect minimized) / strong base reacts with acid of buffer / equilibrium in (i) shifts in forward direction;
Accept OH– added reacts with H+ to form H2O.
\({\text{O}}{{\text{H}}^ - }{\text{(aq)}} + {{\text{H}}_2}{\text{PO}}_4^ - {\text{(aq)}} \to {{\text{H}}_2}{\text{O(l)}} + {\text{HPO}}_4^{2 - }{\text{(aq)}}\);
Ignore state symbols, accept equilibrium sign.
(iii) strong acid/\({{\text{H}}^ + }\) replaced by weak acid (\({{\text{H}}_2}{\text{PO}}_4^ - \), and effect minimized) / strong acid reacts with base of buffer / equilibrium in (i) shifts in reverse direction;
\({{\text{H}}^ + }{\text{(aq)}} + {\text{HPO}}_4^{2 - }{\text{(aq)}} \to {{\text{H}}_2}{\text{PO}}_4^ - {\text{(aq)}}\);
Accept reaction with H3O+.
Ignore state symbols.
(i) \({\text{N}}{{\text{H}}_3}\) weak(er) base/partial dissociation;
\({\text{[O}}{{\text{H}}^ - }{\text{]}} < {\text{0.1(0)}}/{\text{pOH}} > 1{\text{ (thus pH}} < 13/{\text{pH}} + {\text{pOH}} = 14{\text{)}}\);
(ii) around \({\text{pH}} = 5\);
Accept a value between 4 and 6.
strong acid–weak base titration, (thus acidic) / at equivalence point, \({\text{NH}}_4^ + \) present is acidic / \({\text{NH}}_4^ + \rightleftharpoons {\text{N}}{{\text{H}}_3} + {{\text{H}}^ + }\);
(iii) \({\text{N}}{{\text{H}}_3}{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{NH}}_4^ + {\text{(aq)}} + {\text{O}}{{\text{H}}^ - }{\text{(aq)}}\);
Ignore state symbols, but equilibrium sign required.
\({K_{\text{b}}} = \frac{{{\text{[NH}}_4^ + {\text{][O}}{{\text{H}}^ - }{\text{]}}}}{{{\text{[N}}{{\text{H}}_3}{\text{]}}}}\);
(iv) \({\text{[N}}{{\text{H}}_3}{\text{]}} = {\text{[NH}}_4^ + {\text{]}}\);
(v) \({\text{pOH}} = 14.00 - 9.25 = 4.75\);
\({\text{p}}{K_{\text{b}}}{\text{ (}} = {\text{pOH)}} = 4.75\);
\({K_{\text{b}}} = 1.78 \times {10^{ - 5}}\);
Ignore units.
Award [3] for correct final answer.
(vi) optimum/most effective/highest buffer capacity/50%–50% buffer/equally effective as an acidic buffer and a basic buffer / OWTTE;
Examiners report
This was the second least commonly answered question. With the exception of the part on buffer chemistry where very few appreciated what was happening, the question was reasonably well done.
While many candidates gave the correct \({K_{\text{w}}}\) expression, it was not uncommon to either find the value of the constant or \({K_{\text{w}}} = {K_{\text{a}}} \times {K_{\text{b}}}\) given as the answers. A few included \({\text{[}}{{\text{H}}_{\text{2}}}{\text{O]}}\) in the expression. Candidates recognised that increasing the temperature shifts the equilibrium to the right, but most did not explain why, namely to use up some of the heat supplied.
Candidates generally concluded that formation of more \({{\text{H}}^ + }\) and \({\text{O}}{{\text{H}}^ - }\) ions gives a higher value of \({K_{\text{w}}}\). A significant number of candidates were able to state the effect of increasing temperature on the pH of water (it decreases) but failed to explain why. Some simply incorrectly stated that the pH would not change.
Many candidates gave the wrong formulas for the acid and the conjugate base ions of the buffer or offered \({\text{Na}}{{\text{H}}_{\text{2}}}{\text{P}}{{\text{O}}_{\text{4}}}\) and \({\text{N}}{{\text{a}}_{\text{2}}}{\text{HP}}{{\text{O}}_{\text{4}}}\) as the answers. Some candidates gave good answers about the effect of adding a small amount of a strong acid or a strong base, but they could not write correct equations to show these two effects.
Nearly all candidates correctly said that the ammonia solution is a weak base because of partial dissociation and \({\text{[O}}{{\text{H}}^ - }{\text{]}}\) would be less than 0.1 to give a pH less than 13. The majority of candidates correctly identified the pH around 4 – 6 because it is a titration between a strong acid and a weak base. When writing the equation for the reaction of ammonia and water some candidates did not write the equilibrium sign. The \({K_{\text{b}}}\) expression was correct in most cases. However, many did not recognise that at the half-equivalence point both the base and the conjugate acid concentrations are equal. The \({\text{p}}{K_{\text{b}}}\) and \({K_{\text{b}}}\) were correctly calculated from the pH of the solution by many candidates. However, most failed to realize that at the half-equivalence point the capacity of the buffer is optimum.
Define the terms acid and base according to the Brønsted-Lowry theory. Distinguish between a weak base and a strong base. State one example of a weak base.
Weak acids in the environment may cause damage. Identify a weak acid in the environment and outline one of its effects.
The graph below indicates the pH change during the titration of \({\text{20.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) of \({\text{C}}{{\text{H}}_{\text{3}}}{\text{COOH(aq)}}\) with \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ KOH(aq)}}\). From the graph, identify the volume of KOH(aq) and the pH at the equivalence point.
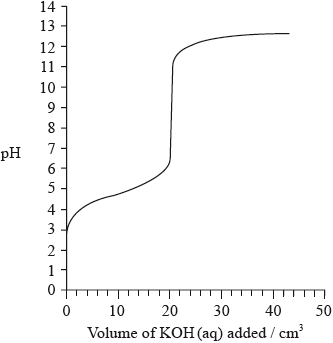
Explain how the graph could be used to determine the \({\text{p}}{K_{\text{a}}}\) of ethanoic acid and determine the \({\text{p}}{K_{\text{a}}}\) value for these data.
Sketch a graph, similar to the graph on the previous page, to indicate the change in pH during a titration of \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ HN}}{{\text{O}}_{\text{3}}}{\text{(aq)}}\) with \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) KOH(aq). On your graph, clearly indicate the starting pH value, the equivalence point, the pH at the equivalence point and the final pH reached.
Describe how an indicator works.
Using Table 16 of the Data Booklet, identify the most appropriate indicator for the titration of ethanoic acid with potassium hydroxide. Explain your choice.
Determine the pH of the solution resulting when \({\text{100 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.50 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ HCl(aq)}}\) is mixed with \({\text{200 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ NaOH(aq)}}\).
Markscheme
Acid: proton/\({{\text{H}}^ + }\) donor and Base: proton/\({{\text{H}}^ + }\) acceptor;
Do not accept \(O{H^ - }\) for base.
Weak base: (base/electrolyte) partially dissociated/ionized (in solution/water) and Strong base: (base/electrolyte assumed to be almost) completely/100% dissociated/ionized (in solution/water) / OWTTE;
\({\text{N}}{{\text{H}}_{\text{3}}}/{\text{C}}{{\text{H}}_{\text{3}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{N}}{{\text{H}}_{\text{2}}}\);
Allow either name or formula or other suitable example.
sulfurous acid/\({{\text{H}}_{\text{2}}}{\text{S}}{{\text{O}}_{\text{3}}}\);
corrodes marble/limestone buildings/statues / leaching in soils / harms/kills
plants;
OR
nitrous acid/\({\text{HN}}{{\text{O}}_{\text{2}}}\);
corrodes marble/limestone buildings/statues / leaching in soils / harms/kills
plants;
OR
carbonic acid/\({{\text{H}}_{\text{2}}}{\text{C}}{{\text{O}}_{\text{3}}}\);
corrodes marble/limestone buildings/statues / acidification of lakes;
Do not allow oxides (e.g. CO2 etc.).
Do not accept just corrodes or damages.
Volume of KOH: 20 (\({\text{c}}{{\text{m}}^{\text{3}}}\));
Allow any value between 20 and 21 (cm3).
pH at the equivalence point: 8.0–10.0;
At half-equivalence point \({\text{[C}}{{\text{H}}_{\text{3}}}{\text{COOH]}} = {\text{[C}}{{\text{H}}_{\text{3}}}{\text{CO}}{{\text{O}}^ - }{\text{]}}\) so \({\text{pH}} = {\text{p}}{K_{\text{a}}}\);
\({\text{p}}{K_{\text{a}}} = 4.7\);
Accept in range 4.2 to 5.2.
M2 can only be scored if M1 correct (i.e. no marks for just Data Booklet value of 4.76).
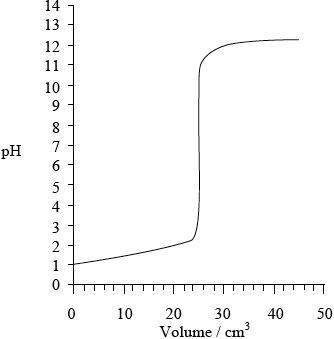
Starting pH: 1;
Equivalence point: \({\text{pH}} = 7\) and 25 \({\text{c}}{{\text{m}}^{\text{3}}}\);
Final pH reached: 12–13;
correct curve shape;
Do not award M4 if turn in curve is seen at low volumes (suggesting weak acid–strong base titration).
Award [4] if values corresponding to M1, M2 and M3 are labelled on graph (e.g using X) and correct shape of curve shown.
HIn is a weak acid / weak base;

Award [2] for M2 alone.
in base equilibrium moves to right / in acid equilibrium moves to left;
phenolphthalein;
indicator colour change occurs in range of pH at the equivalence point / OWTTE;
M2 can be scored independently even if indicator is incorrect.
\(n{\text{(HCl)}} = (0.100 \times 0.50) = 0.050{\text{ (mol)}}\);
\(n{\text{(NaOH)}} = (0.200 \times 0.10) = 0.020{\text{ (mol)}}\);
\(n{{\text{(HCl)}}_{{\text{remaining}}}} = (0.050 - 0.020) = 0.030{\text{ (mol)}}\);
\({\text{[HCl]}} = \left( {\frac{{0.030}}{{0.30}}} \right) = 0.10{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({\text{pH}} = 1.0\);
Award [2 max] for just pH = 1.0 without working.
Examiners report
This was a popular question and often was well answered by candidates. In (a) (i) most candidates knew the formal definitions of an acid and a base and most could distinguish between a weak base and a strong base. Ammonia was generally given as a suitable example of a weak base. Some of the weaker students gave sodium hydroxide incorrectly as an example of a weak base which was quite surprising at HL.
In (ii), common mistakes included nitric acid and this question proved to be problematic for candidates. There were a number of G2 comments expressing some concern at asking this style of question, though this is a clear Aim 8 type question that should be explored in the formal teaching programme.
(iii) was well done.
Candidates rarely got (iv) correct.
In (v) most candidates scored either two or three, but often an incorrect shape of the curve was given.
In (b), few could describe how an indicator works and the equilibrium sign was sometimes omitted.
In (ii), phenolphthalein was usually identified as an appropriate indicator.
In (d), candidates who were able to think logically about all this did well; others scattered figures across the page and became hopelessly muddled. Often an incorrect answer of \({\text{pH}} = 7.0\) was seen.
Graphing is an important tool in the study of rates of chemical reactions.
The graph represents the titration of 25.00 cm3 of 0.100 mol dm−3 aqueous ethanoic acid with 0.100 mol dm−3 aqueous sodium hydroxide.
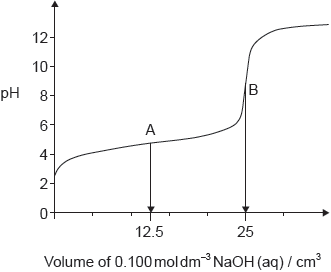
Deduce the major species, other than water and sodium ions, present at points A and B during the titration.
Calculate the pH of 0.100 mol dm−3 aqueous ethanoic acid.
Ka = 1.74 × 10−5
Outline, using an equation, why sodium ethanoate is basic.
Predict whether the pH of an aqueous solution of ammonium chloride will be greater than, equal to or less than 7 at 298 K.
Formulate the equation for the reaction of nitrogen dioxide, NO2, with water to form two acids.
Formulate the equation for the reaction of one of the acids produced in (e)(i) with calcium carbonate.
Markscheme
A: CH3COOH/ethanoic/acetic acid AND CH3COO–/ethanoate/acetate ions
B: CH3COO–/ethanoate/acetate ions
Penalize “sodium ethanoate/acetate” instead of “ethanoate/acetate ions” only once.
[2 marks]
\({K_{\text{a}}} = 1.74 \times {10^{ - 5}} = \frac{{{{{\text{[}}{{\text{H}}^ + }{\text{]}}}^2}}}{{0.10}}\)
OR
[H+] = 1.32 × 10–3 «mol dm–3»
«pH =» 2.88
Accept [2] for correct final answer.
[2 marks]
«forms weak acid and strong base, thus basic»
CH3COO–(aq) + H2O(l) \( \rightleftharpoons \) CH3COOH(aq) + OH–(aq)
Accept → for \( \rightleftharpoons \).
[1 mark]
less than 7
[1 mark]
2NO2(g) + H2O(l) → HNO2(aq) + HNO3(aq)
[1 mark]
2HNO2(aq) + CaCO3(s) → Ca(NO2)2(aq) + CO2(g) + H2O(l)
OR
2HNO3(aq) + CaCO3(s) → Ca(NO3)2(aq) + CO2(g) + H2O(l)
[1 mark]
Examiners report
Limescale, CaCO3(s), can be removed from water kettles by using vinegar, a dilute solution of ethanoic acid, CH3COOH(aq).
Predict, giving a reason, a difference between the reactions of the same concentrations of hydrochloric acid and ethanoic acid with samples of calcium carbonate.
Dissolved carbon dioxide causes unpolluted rain to have a pH of approximately 5, but other dissolved gases can result in a much lower pH. State one environmental effect of acid rain.
Write an equation to show ammonia, NH3, acting as a Brønsted–Lowry base and a different equation to show it acting as a Lewis base.
Determine the pH of 0.010 mol dm−3 2,2-dimethylpropanoic acid solution.
Ka (2,2-dimethylpropanoic acid) = 9.333 × 10−6
Explain, using appropriate equations, how a suitably concentrated solution formed by the partial neutralization of 2,2-dimethylpropanoic acid with sodium hydroxide acts as a buffer solution.
Markscheme
slower rate with ethanoic acid
OR
smaller temperature rise with ethanoic acid
[H+] lower
OR
ethanoic acid is weak
OR
ethanoic acid is partially dissociated
Accept experimental observations such as “slower bubbling” or “feels less warm”.
[2 marks]
Any one of:
corrosion of materials/metals/carbonate materials
destruction of plant/aquatic life
«indirect» effect on human health
Accept “lowering pH of oceans/lakes/waterways”.
[1 mark]
Brønsted–Lowry base:
NH3 + H+ → NH4+
Lewis base:
NH3 + BF3 → H3NBF3
Accept “AlCl3 as an example of Lewis acid”.
Accept other valid equations such as Cu2+ + 4NH3 → [Cu(NH3)4]2+.
[2 marks]
[H+] «\( = \sqrt {{{\text{K}}_{\text{a}}} \times \left[ {{{\text{C}}_5}{{\text{H}}_{10}}{{\text{O}}_2}} \right]} = \sqrt {9.333 \times {{10}^{ - 6}} \times 0.010} {\text{ }}\)» = 3.055 × 10–4 «mol dm–3»
«pH =» 3.51
Accept “pH = 3.52”.
Award [2] for correct final answer.
Accept other calculation methods.
[2 marks]
(CH3)3CCOOH(aq) + OH–(aq) → (CH3)3CCOO–(aq) + H2O(l)
OR
(CH3)3CCOOH(aq) + OH–(aq) \( \rightleftharpoons \) (CH3)3CCOO–(aq) + H2O(l) AND addition of alkali causes equilibrium to move to right
(CH3)3CCOO–(aq) + H+(aq) → (CH3)3CCOOH(aq)
OR
(CH3)3CCOO–(aq) + H+(aq) \( \rightleftharpoons \) (CH3)3CCOOH(aq) AND addition of acid causes equilibrium to move to right
Accept “HA” for the acid.
Award [1 max] for correct explanations of buffering with addition of acid AND base without equilibrium equations.
[2 marks]
Examiners report
Acid–base chemistry can play a major role in chemical and biological processes.
White vinegar, which contains ethanoic acid, CH3COOH, can be used as a cleaning agent to dissolve mineral deposits from coffee machines.
Buffer solutions play a pivotal role in solution chemistry.
Acid–base indicators are often organic dyes.
Ammonia, NH3, can be used to clean ovens. The concentration of hydroxide ions, OH–(aq), in a solution of ammonia is \({\text{3.98}} \times {\text{1}}{{\text{0}}^{ - 3}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\). Calculate its pH, correct to one decimal place, at 298 K.
Define an acid according to the Brønsted–Lowry theory and the Lewis theory.
Brønsted–Lowry theory:
Lewis theory:
Ethanoic acid is an example of a weak acid. Distinguish between a strong acid and a weak acid in terms of the extent of dissociation.
State whether the following mixtures, in the appropriate molar ratios, can be classified as buffer solutions. Show your answer by stating yes or no in the table below.

Describe qualitatively the action of an acid–base indicator.
Using Table 16 of the Data Booklet, identify the most appropriate indicator for the titration of ethanoic acid with sodium hydroxide. Explain your choice.
\({\text{150 c}}{{\text{m}}^{\text{3}}}\) of \({\text{5.00}} \times {\text{1}}{{\text{0}}^{ - 1}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl (aq) is mixed with \({\text{300 c}}{{\text{m}}^{\text{3}}}\) of \({\text{2.03}} \times {\text{1}}{{\text{0}}^{ - 1}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) NaOH(aq). Determine the pH of the solution, correct to two decimal places.
Markscheme
\([{{\text{H}}_3}{{\text{O}}^ + }] = \frac{{{K_{\text{w}}}}}{{[{\text{O}}{{\text{H}}^ - }]}} = \frac{{(1.00 \times {{10}^{ - 14}})}}{{(3.98 \times {{10}^{ - 3}})}} = 2.51 \times {10^{ - 12}}{\text{ }}({\text{mol}}\,{\text{d}}{{\text{m}}^{ - 3}})\);
\({\text{pH}}\left( { = - \log [{{\text{H}}_3}{{\text{O}}^ + }] = - \log (2.51 \times {{10}^{ - 12}})} \right) = 11.6\);
OR
\({\text{pOH}} = \left( { - \log (3.98 \times {{10}^{ - 3}}) = } \right){\text{ }}2.4\);
\({\text{pH}} = (14.00 - 2.40) = 11.6\);
Award [2] for correct final answer.
Allow correct use of H+ instead of \({H_3}{O^ + }\) throughout.
Brønsted-Lowry theory:
proton/\({{\text{H}}^ + }\) donor;
Lewis theory:
electron pair acceptor;
Strong acid: acid/electrolyte (assumed to be almost) completely/100% dissociated/ionized (in solution/water) / OWTTE and Weak acid:
acid/electrolyte partially dissociated/ionized (in solution/water) / OWTTE;
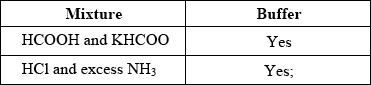
Award [1] for both “yes”.
Award [0] for any “no”.
\(\begin{array}{*{20}{l}} {{\text{HIn(aq)}} \rightleftharpoons {{\text{H}}^ + }{\text{(aq)}} + {\text{I}}{{\text{n}}^ - }{\text{(aq) /}}}&{{\text{HIn(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{I}}{{\text{n}}^ - }{\text{(aq)}} + {{\text{H}}_3}{{\text{O}}^ + }{\text{(aq)}}} \\ {{\text{Colour}}\,{\text{A Colour}}\,{\text{B}}}&{{\text{Colour}}\,{\text{A Colour}}\,{\text{B}}} \end{array}\);
Allow statement such as solution of weak acid with different colours for conjugate base/In\(^ - \)(aq) and undissociated acid/HIn(aq) / OWTTE.
Equilibrium sign required.
Ignore state symbols.
Allow corresponding argument for an indicator as a weak base.
for example, BOH(aq) \( \to \) B\(^ + \)(aq) + OH\(^ - \)(aq) etc.
in acid/presence of \({{\text{H}}^ + }\) equilibrium lies to left (so colour A);
in alkali/base/presence of \({\text{O}}{{\text{H}}^ - }\) equilibrium lies to right (so colour B);
colour changes/end point when \({\text{[HIn(aq)]}} \approx {\text{[I}}{{\text{n}}^ - }{\text{(aq)]}}\);
phenolphthalein/phenol red;
indicator changes colour in range of pH at equivalence point which is above 7 / OWTTE;
M2 can be scored independently even if indicator is incorrect.
Accept it is a titration of weak acid with a strong base for M2.
\(n{\text{(HCl) }}\left( { = \frac{{(150 \times 5.00 \times {{10}^{ - 1}})}}{{(1000)}}} \right) = 7.50 \times {10^{ - 2}}{\text{ (mol)}}\) and
\(n{\text{(NaOH) }}\left( {\frac{{(300 \times 2.03 \times {{10}^{ - 1}})}}{{(1000)}}} \right) = 6.09 \times {10^{ - 2}}{\text{ (mol)}}\);
\(n{{\text{(HCl)}}_{{\text{remaining}}}}{\text{ }}\left( { = (7.50 - 6.09) \times {{10}^{ - 2}}} \right) = 1.41 \times {10^{ - 2}}{\text{ (mol)}}\);
\({\text{[HCl]}} = (1.41 \times {10^{ - 2}})(1000)/(450) = 3.13 \times {10^{ - 2}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ )}}\);
pH =1.50;
Award [4] for correct final answer.
Award [3 max] for pH = –log (1.41 \( \times \) 10−2 ) =1.85 .
Examiners report
Most candidates calculated the pH of ammonia solution correctly and also the pH of the buffer solution in part (c) (ii). Most students could explain why a solution of the chromium complex is coloured. The difficult part in this question for many was to state and explain whether the salts in solution were acidic, basic or neutral. (e) again caused difficulties for candidates, similar to previous sessions, though many scored some marks for stating acidic. (ii) was very poorly done and M2 was effectively a dead mark.
Most candidates calculated the pH of ammonia solution correctly and also the pH of the buffer solution in part (c) (ii). Most students could explain why a solution of the chromium complex is coloured. The difficult part in this question for many was to state and explain whether the salts in solution were acidic, basic or neutral. (e) again caused difficulties for candidates, similar to previous sessions, though many scored some marks for stating acidic. (ii) was very poorly done and M2 was effectively a dead mark.
Most candidates calculated the pH of ammonia solution correctly and also the pH of the buffer solution in part (c) (ii). Most students could explain why a solution of the chromium complex is coloured. The difficult part in this question for many was to state and explain whether the salts in solution were acidic, basic or neutral. (e) again caused difficulties for candidates, similar to previous sessions, though many scored some marks for stating acidic. (ii) was very poorly done and M2 was effectively a dead mark.
Most candidates calculated the pH of ammonia solution correctly and also the pH of the buffer solution in part (c) (ii). Most students could explain why a solution of the chromium complex is coloured. The difficult part in this question for many was to state and explain whether the salts in solution were acidic, basic or neutral. (e) again caused difficulties for candidates, similar to previous sessions, though many scored some marks for stating acidic. (ii) was very poorly done and M2 was effectively a dead mark.
Most candidates calculated the pH of ammonia solution correctly and also the pH of the buffer solution in part (c) (ii). Most students could explain why a solution of the chromium complex is coloured. The difficult part in this question for many was to state and explain whether the salts in solution were acidic, basic or neutral. (e) again caused difficulties for candidates, similar to previous sessions, though many scored some marks for stating acidic. (ii) was very poorly done and M2 was effectively a dead mark.
Most candidates calculated the pH of ammonia solution correctly and also the pH of the buffer solution in part (c) (ii). Most students could explain why a solution of the chromium complex is coloured. The difficult part in this question for many was to state and explain whether the salts in solution were acidic, basic or neutral. (e) again caused difficulties for candidates, similar to previous sessions, though many scored some marks for stating acidic. (ii) was very poorly done and M2 was effectively a dead mark.
Most candidates calculated the pH of ammonia solution correctly and also the pH of the buffer solution in part (c) (ii). Most students could explain why a solution of the chromium complex is coloured. The difficult part in this question for many was to state and explain whether the salts in solution were acidic, basic or neutral. (e) again caused difficulties for candidates, similar to previous sessions, though many scored some marks for stating acidic. (ii) was very poorly done and M2 was effectively a dead mark.
A student used a pH meter to measure the pH of different samples of water at 298 K.
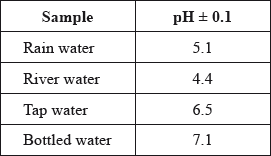
Use the data in the table to identify the most acidic water sample.
Calculate the percentage uncertainty in the measured pH of the rain water sample.
Determine the ratio of \({\text{[}}{{\text{H}}^ + }{\text{]}}\) in bottled water to that in rain water.
\[\frac{{[{H^ + }]{\text{ }}in{\text{ }}bottled{\text{ }}water}}{{[{H^ + }]{\text{ }}in{\text{ }}rain{\text{ }}water}}\]
Determine the concentration of hydroxide ions in the sample of river water.
The acidity of non-polluted rain water is caused by dissolved carbon dioxide. State an equation for the reaction of carbon dioxide with water.
Markscheme
river (water);
\(\left( {\frac{{0.1}}{{5.1}} \times 100 = } \right){\text{ }}2\% \);
recognition that values differ by 2 pH units / calculation of both \({\text{[}}{{\text{H}}^ + }{\text{]}}\) values;
\(({\text{ratio}} = ){\text{ }}1:100/\frac{1}{{100}}/{10^{ - 2}}/0.01\);
Award [2] for correct final answer.
Award [1 max] for 100:1/100/102.
\({\text{pOH}} = (14.0 - 4.4 = ){\text{ }}9.6/{\text{[}}{{\text{H}}^ + }{\text{]}} = 4 \times {10^{ - 5}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
Accept [H+] = 3.98 \( \times \) 10–5 (mol dm–3).
\({\text{[O}}{{\text{H}}^ - }{\text{]}} = 3 \times {10^{ - 10}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
Accept 2.51 \( \times \) 10–10 (mol dm–3).
Award [2] for correct final answer.
\({\text{C}}{{\text{O}}_2} + {{\text{H}}_2}{\text{O}} \rightleftharpoons {\text{HCO}}_3^ - + {{\text{H}}^ + }/{\text{C}}{{\text{O}}_2} + {\text{2}}{{\text{H}}_2}{\text{O}} \rightleftharpoons {\text{HCO}}_3^ - + {{\text{H}}_2}{{\text{O}}^ + }/{\text{C}}{{\text{O}}_2} + {{\text{H}}_2}{\text{O}} \rightleftharpoons {{\text{H}}_2}{\text{C}}{{\text{O}}_3}\);
Do not penalize missing reversible arrow.
Do not accept equations with the carbonate ion as a product.
Examiners report
A very well answered question.
The majority of candidates calculated the percentage uncertainty correctly, however, more than half of them did not pay attention to stating the answer to the appropriate number of significant figures. Some candidates used river water data instead of rain water.
More than half of the candidates calculated the correct ratio of hydrogen ion concentration. The majority of these candidates calculated the concentration of hydrogen ions in both samples, instead of simply using the difference of 2 pH units.
Generally well answered. Some students only scored one mark, stopping at the calculation of the pOH or the concentration of hydrogen.
About half the candidates wrote correct products, however, most of the candidates did not use reversible arrows. Several variations of incorrect products were given including \({{\text{H}}_{\text{2}}}{{\text{O}}_{\text{2}}}\) and CO.
Antimony, Sb, forms a fluoride, \({\text{Sb}}{{\text{F}}_{\text{5}}}\).
The equilibrium that occurs when antimony(V) fluoride is dissolved in liquid hydrogen fluoride can be represented by the equation below.
\[{\text{Sb}}{{\text{F}}_5}{\text{(s)}} + {\text{2HF(l)}} \rightleftharpoons {\text{SbF}}_6^ - {\text{(sol)}} + {{\text{H}}_2}{{\text{F}}^ + }{\text{(sol)}}\]
Outline how the following factors account for the fact that HCl is a strong acid and HF is a weak acid.
Some students were provided with a \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of a monobasic acid, HQ, and given the problem of determining whether HQ was a weak acid or a strong acid.
The second problem set for the students was to determine the acid dissociation constant, \({K_{\text{a}}}\), of the acid HQ and its \({\text{p}}{K_{\text{a}}}\).
State the element that you would expect to have chemical properties most similar to those of antimony.
Describe the relationship between \({\text{Sb}}{{\text{F}}_{\text{5}}}\) and \({\text{SbF}}_6^ - \) in terms of the Lewis theory of acids.
Explain the behaviour of HF in terms of the Brønsted–Lowry theory of acids.
The strength of the hydrogen–halogen bond.
The interaction between an undissociated hydrogen halide molecule and a water molecule.
Neelu and Charles decided to solve the problem by determining the volume of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide solution needed to neutralize \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of the acid. Outline whether this was a good choice.
Identify one indicator that could be used when titrating aqueous sodium hydroxide with both a strong acid and a weak acid, and outline the reason for your choice.
Indicator:
Reason:
Neelu and Charles decided to compare the volume of sodium hydroxide solution needed with those required by known \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) strong and weak acids. Unfortunately they chose sulfuric acid as the strong acid. Outline why this was an unsuitable choice.
Francisco and Shamiso decided to measure the pH of the initial solution, HQ, and they found that its pH was 3.7. Deduce, giving a reason, the strength (weak or strong) of the acid HQ.
Explain how the \({\text{p}}{K_{\text{a}}}\) could be determined from a graph of pH against the volume of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide added.
Francisco and Shamiso found that the pH of the initial \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution was 3.7. However, this reading was inaccurate because they forgot to wash the pH probe. Calculate the \({\text{p}}{K_{\text{a}}}\) of HQ using the reading they obtained.
Markscheme
arsenic/As;
Accept bismuth/Bi.
\({\text{Sb}}{{\text{F}}_{\text{5}}}\) accepts an electron pair (from \({{\text{F}}^ - }\)) / \({\text{SbF}}_6^ - \) donates an electron pair (to \(H_2F^ +\));
\({\text{Sb}}{{\text{F}}_{\text{5}}}\) acts as a Lewis acid / \({\text{SbF}}_6^ - \) acts as a Lewis base;
one HF donates a \({{\text{H}}^ + }\)/proton and the other accepts a \({{\text{H}}^ + }\)/proton;
HF acts as both a Brønsted–Lowry acid and a Brønsted–Lowry base;
Award [1 max] for correct description of HF acting as a Brønsted–Lowry acid or base.
H–F bond stronger than H–Cl bond / H–Cl bond weaker than H–F bond;
H–F can hydrogen bond to water and H–Cl cannot;
not a good choice / poor choice;
requires same volume of base / the amount/volume to react/for neutralization does not depend on the acid strength;
phenolphthalein / phenol red;
pH at equivalence point 7 or above;
Accept pH range for colour change/end-point corresponds to rapid change in pH.
sulfuric acid is diprotic/dibasic/liberates two protons/\({{\text{H}}^ + }\);
Accept “reacts with 2 moles of alkali/base”.
weak;
strong \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) acid has a pH of 1/lower than that observed;
Accept “pH value of 3.7 means that it produces only 10–3.7/2.0 \( \times \) 10–4 [H+] in water”.
when volume of alkali is half equivalence volume/volume required for neutralization;
\({\text{p}}{K_{\text{a}}}\) is equal to the pH;
\([{{\text{H}}^ + }] = {10^{ - 3.7}} = 2.00 \times {10^{ - 4}}{\text{ }}({\text{mol}}\,{\text{d}}{{\text{m}}^{ - 3}})\);
\({K_{\text{a}}} = \frac{{[{{\text{H}}^ + }][{{\text{Q}}^ - }]}}{{[{\text{HQ}}]}} = \frac{{{{(2.00 \times {{10}^{ - 4}})}^2}}}{{0.100}}\);
\( = 3.98 \times {10^{ - 7}}\);
\({\text{p}}{K_{\text{a}}} = 6.4\);
Award [4] for correct final answer.
Examiners report
Most students could identify an element which would be expected to have similar properties to antimony and the reaction between its fluoride and hydrogen fluoride was generally well interpreted in terms of acid-base theories, though hardly any students realized that HF is acting as both a base (to give \({{\text{H}}_{\text{2}}}{{\text{F}}^ + }\)) and an acid (to give \({{\text{F}}^ - }\) which complexes with \({\text{As}}{{\text{F}}_{\text{5}}}\)). The significance of the strength of the hydrogen-halogen bond on the strength of the hydrogen halides was often appreciated though very few seemed to realize that HF hydrogen bonds to water whereas HCl does not. Many students think that weak acids require a smaller volume of alkali for neutralization than strong acids of equal concentration, though most could correctly identify an appropriate indicator for the titration and justify their choice. Most realized that sulfuric acid was dibasic, were aware of the significance of the pH at the half equivalence point and correctly identified HQ as a weak acid, though justifying this proved more of a challenge. Quite a few students gained full credit the calculation of the \({\text{p}}{K_{\text{a}}}\) from the initial pH and many gained some marks for the calculation of the pH of the buffer system.
Most students could identify an element which would be expected to have similar properties to antimony and the reaction between its fluoride and hydrogen fluoride was generally well interpreted in terms of acid-base theories, though hardly any students realized that HF is acting as both a base (to give \({{\text{H}}_{\text{2}}}{{\text{F}}^ + }\)) and an acid (to give \({{\text{F}}^ - }\) which complexes with \({\text{As}}{{\text{F}}_{\text{5}}}\)). The significance of the strength of the hydrogen-halogen bond on the strength of the hydrogen halides was often appreciated though very few seemed to realize that HF hydrogen bonds to water whereas HCl does not. Many students think that weak acids require a smaller volume of alkali for neutralization than strong acids of equal concentration, though most could correctly identify an appropriate indicator for the titration and justify their choice. Most realized that sulfuric acid was dibasic, were aware of the significance of the pH at the half equivalence point and correctly identified HQ as a weak acid, though justifying this proved more of a challenge. Quite a few students gained full credit the calculation of the \({\text{p}}{K_{\text{a}}}\) from the initial pH and many gained some marks for the calculation of the pH of the buffer system.
Most students could identify an element which would be expected to have similar properties to antimony and the reaction between its fluoride and hydrogen fluoride was generally well interpreted in terms of acid-base theories, though hardly any students realized that HF is acting as both a base (to give \({{\text{H}}_{\text{2}}}{{\text{F}}^ + }\)) and an acid (to give \({{\text{F}}^ - }\) which complexes with \({\text{As}}{{\text{F}}_{\text{5}}}\)). The significance of the strength of the hydrogen-halogen bond on the strength of the hydrogen halides was often appreciated though very few seemed to realize that HF hydrogen bonds to water whereas HCl does not. Many students think that weak acids require a smaller volume of alkali for neutralization than strong acids of equal concentration, though most could correctly identify an appropriate indicator for the titration and justify their choice. Most realized that sulfuric acid was dibasic, were aware of the significance of the pH at the half equivalence point and correctly identified HQ as a weak acid, though justifying this proved more of a challenge. Quite a few students gained full credit the calculation of the \({\text{p}}{K_{\text{a}}}\) from the initial pH and many gained some marks for the calculation of the pH of the buffer system.
Most students could identify an element which would be expected to have similar properties to antimony and the reaction between its fluoride and hydrogen fluoride was generally well interpreted in terms of acid-base theories, though hardly any students realized that HF is acting as both a base (to give \({{\text{H}}_{\text{2}}}{{\text{F}}^ + }\)) and an acid (to give \({{\text{F}}^ - }\) which complexes with \({\text{As}}{{\text{F}}_{\text{5}}}\)). The significance of the strength of the hydrogen-halogen bond on the strength of the hydrogen halides was often appreciated though very few seemed to realize that HF hydrogen bonds to water whereas HCl does not. Many students think that weak acids require a smaller volume of alkali for neutralization than strong acids of equal concentration, though most could correctly identify an appropriate indicator for the titration and justify their choice. Most realized that sulfuric acid was dibasic, were aware of the significance of the pH at the half equivalence point and correctly identified HQ as a weak acid, though justifying this proved more of a challenge. Quite a few students gained full credit the calculation of the \({\text{p}}{K_{\text{a}}}\) from the initial pH and many gained some marks for the calculation of the pH of the buffer system.
Most students could identify an element which would be expected to have similar properties to antimony and the reaction between its fluoride and hydrogen fluoride was generally well interpreted in terms of acid-base theories, though hardly any students realized that HF is acting as both a base (to give \({{\text{H}}_{\text{2}}}{{\text{F}}^ + }\)) and an acid (to give \({{\text{F}}^ - }\) which complexes with \({\text{As}}{{\text{F}}_{\text{5}}}\)). The significance of the strength of the hydrogen-halogen bond on the strength of the hydrogen halides was often appreciated though very few seemed to realize that HF hydrogen bonds to water whereas HCl does not. Many students think that weak acids require a smaller volume of alkali for neutralization than strong acids of equal concentration, though most could correctly identify an appropriate indicator for the titration and justify their choice. Most realized that sulfuric acid was dibasic, were aware of the significance of the pH at the half equivalence point and correctly identified HQ as a weak acid, though justifying this proved more of a challenge. Quite a few students gained full credit the calculation of the \({\text{p}}{K_{\text{a}}}\) from the initial pH and many gained some marks for the calculation of the pH of the buffer system.
Most students could identify an element which would be expected to have similar properties to antimony and the reaction between its fluoride and hydrogen fluoride was generally well interpreted in terms of acid-base theories, though hardly any students realized that HF is acting as both a base (to give \({{\text{H}}_{\text{2}}}{{\text{F}}^ + }\)) and an acid (to give \({{\text{F}}^ - }\) which complexes with \({\text{As}}{{\text{F}}_{\text{5}}}\)). The significance of the strength of the hydrogen-halogen bond on the strength of the hydrogen halides was often appreciated though very few seemed to realize that HF hydrogen bonds to water whereas HCl does not. Many students think that weak acids require a smaller volume of alkali for neutralization than strong acids of equal concentration, though most could correctly identify an appropriate indicator for the titration and justify their choice. Most realized that sulfuric acid was dibasic, were aware of the significance of the pH at the half equivalence point and correctly identified HQ as a weak acid, though justifying this proved more of a challenge. Quite a few students gained full credit the calculation of the \({\text{p}}{K_{\text{a}}}\) from the initial pH and many gained some marks for the calculation of the pH of the buffer system.
Most students could identify an element which would be expected to have similar properties to antimony and the reaction between its fluoride and hydrogen fluoride was generally well interpreted in terms of acid-base theories, though hardly any students realized that HF is acting as both a base (to give \({{\text{H}}_{\text{2}}}{{\text{F}}^ + }\)) and an acid (to give \({{\text{F}}^ - }\) which complexes with \({\text{As}}{{\text{F}}_{\text{5}}}\)). The significance of the strength of the hydrogen-halogen bond on the strength of the hydrogen halides was often appreciated though very few seemed to realize that HF hydrogen bonds to water whereas HCl does not. Many students think that weak acids require a smaller volume of alkali for neutralization than strong acids of equal concentration, though most could correctly identify an appropriate indicator for the titration and justify their choice. Most realized that sulfuric acid was dibasic, were aware of the significance of the pH at the half equivalence point and correctly identified HQ as a weak acid, though justifying this proved more of a challenge. Quite a few students gained full credit the calculation of the \({\text{p}}{K_{\text{a}}}\) from the initial pH and many gained some marks for the calculation of the pH of the buffer system.
Most students could identify an element which would be expected to have similar properties to antimony and the reaction between its fluoride and hydrogen fluoride was generally well interpreted in terms of acid-base theories, though hardly any students realized that HF is acting as both a base (to give \({{\text{H}}_{\text{2}}}{{\text{F}}^ + }\)) and an acid (to give \({{\text{F}}^ - }\) which complexes with \({\text{As}}{{\text{F}}_{\text{5}}}\)). The significance of the strength of the hydrogen-halogen bond on the strength of the hydrogen halides was often appreciated though very few seemed to realize that HF hydrogen bonds to water whereas HCl does not. Many students think that weak acids require a smaller volume of alkali for neutralization than strong acids of equal concentration, though most could correctly identify an appropriate indicator for the titration and justify their choice. Most realized that sulfuric acid was dibasic, were aware of the significance of the pH at the half equivalence point and correctly identified HQ as a weak acid, though justifying this proved more of a challenge. Quite a few students gained full credit the calculation of the \({\text{p}}{K_{\text{a}}}\) from the initial pH and many gained some marks for the calculation of the pH of the buffer system.
Most students could identify an element which would be expected to have similar properties to antimony and the reaction between its fluoride and hydrogen fluoride was generally well interpreted in terms of acid-base theories, though hardly any students realized that HF is acting as both a base (to give \({{\text{H}}_{\text{2}}}{{\text{F}}^ + }\)) and an acid (to give \({{\text{F}}^ - }\) which complexes with \({\text{As}}{{\text{F}}_{\text{5}}}\)). The significance of the strength of the hydrogen-halogen bond on the strength of the hydrogen halides was often appreciated though very few seemed to realize that HF hydrogen bonds to water whereas HCl does not. Many students think that weak acids require a smaller volume of alkali for neutralization than strong acids of equal concentration, though most could correctly identify an appropriate indicator for the titration and justify their choice. Most realized that sulfuric acid was dibasic, were aware of the significance of the pH at the half equivalence point and correctly identified HQ as a weak acid, though justifying this proved more of a challenge. Quite a few students gained full credit the calculation of the \({\text{p}}{K_{\text{a}}}\) from the initial pH and many gained some marks for the calculation of the pH of the buffer system.
Most students could identify an element which would be expected to have similar properties to antimony and the reaction between its fluoride and hydrogen fluoride was generally well interpreted in terms of acid-base theories, though hardly any students realized that HF is acting as both a base (to give \({{\text{H}}_{\text{2}}}{{\text{F}}^ + }\)) and an acid (to give \({{\text{F}}^ - }\) which complexes with \({\text{As}}{{\text{F}}_{\text{5}}}\)). The significance of the strength of the hydrogen-halogen bond on the strength of the hydrogen halides was often appreciated though very few seemed to realize that HF hydrogen bonds to water whereas HCl does not. Many students think that weak acids require a smaller volume of alkali for neutralization than strong acids of equal concentration, though most could correctly identify an appropriate indicator for the titration and justify their choice. Most realized that sulfuric acid was dibasic, were aware of the significance of the pH at the half equivalence point and correctly identified HQ as a weak acid, though justifying this proved more of a challenge. Quite a few students gained full credit the calculation of the \({\text{p}}{K_{\text{a}}}\) from the initial pH and many gained some marks for the calculation of the pH of the buffer system.
Most students could identify an element which would be expected to have similar properties to antimony and the reaction between its fluoride and hydrogen fluoride was generally well interpreted in terms of acid-base theories, though hardly any students realized that HF is acting as both a base (to give \({{\text{H}}_{\text{2}}}{{\text{F}}^ + }\)) and an acid (to give \({{\text{F}}^ - }\) which complexes with \({\text{As}}{{\text{F}}_{\text{5}}}\)). The significance of the strength of the hydrogen-halogen bond on the strength of the hydrogen halides was often appreciated though very few seemed to realize that HF hydrogen bonds to water whereas HCl does not. Many students think that weak acids require a smaller volume of alkali for neutralization than strong acids of equal concentration, though most could correctly identify an appropriate indicator for the titration and justify their choice. Most realized that sulfuric acid was dibasic, were aware of the significance of the pH at the half equivalence point and correctly identified HQ as a weak acid, though justifying this proved more of a challenge. Quite a few students gained full credit the calculation of the \({\text{p}}{K_{\text{a}}}\) from the initial pH and many gained some marks for the calculation of the pH of the buffer system.
A student decided to determine the molecular mass of a solid monoprotic acid, HA, by titrating a solution of a known mass of the acid.
The following recordings were made.
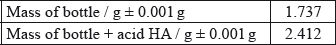
To investigate the effect of temperature on the effectiveness of a buffer solution, the student placed \({\text{20.0 c}}{{\text{m}}^{\text{3}}}\) of the buffer solution in a water bath at 24 °C. He added small portions of hydrochloric acid, stirring after each addition, until a total of \({\text{10 c}}{{\text{m}}^{\text{3}}}\) was added, and measured the pH continuously during the addition. The procedure was repeated at different temperatures and the results are shown in the following graph.

Determine the molecular formula of HA.
State what is meant by a buffer solution.
With reference to the graph on page 4, describe the effect of increasing temperature on the effectiveness of the buffer solution.
Markscheme
\(\left( {\frac{{\text{M}}}{{{\text{Mass of }}{{\text{C}}_4}{{\text{H}}_4}{\text{O}}}} = } \right){\text{ }}\frac{{139}}{{68.08}} = 2\);
\({{\text{C}}_8}{{\text{H}}_8}{{\text{O}}_2}\);
Award [2] for correct final answer.
solution which resists change in pH / changes pH slightly / keeps pH constant / OWTTE;
when small amounts of acid or base are added;
less effective at higher temperatures / more effective between 24 °C and 40 °C than > 40 °C;
pH changes more if the same volume of acid is added at high(er) temperature / OWTTE;
Examiners report
Errors were carried forward in the marking of (d).
The common error in defining a buffer solution in (f) (i) was to omit “small” in the addition of acid or alkali whilst in (ii) candidates needed to be more specific about the volume of acid added for full credit.
The common error in defining a buffer solution in (f) (i) was to omit “small” in the addition of acid or alkali whilst in (ii) candidates needed to be more specific about the volume of acid added for full credit.
A group of students investigated the rate of the reaction between aqueous sodium thiosulfate and hydrochloric acid according to the equation below.
\[{\text{N}}{{\text{a}}_2}{{\text{S}}_2}{{\text{O}}_3}{\text{(aq)}} + {\text{2HCl(aq)}} \to {\text{2NaCl(aq)}} + {\text{S}}{{\text{O}}_2}{\text{(g)}} + {\text{S(s)}} + {{\text{H}}_2}{\text{O(l )}}\]
The two reagents were rapidly mixed together in a beaker and placed over a mark on a piece of paper. The time taken for the precipitate of sulfur to obscure the mark when viewed through the reaction mixture was recorded.
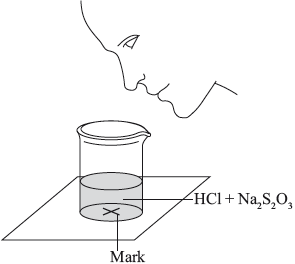
Initially they measured out \({\text{10.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.500 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) hydrochloric acid and then added \({\text{40.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.0200 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) aqueous sodium thiosulfate. The mark on the paper was obscured 47 seconds after the solutions were mixed.
One proposed mechanism for this reaction is:
\({{\text{S}}_2}{\text{O}}_3^{2 - }{\text{(aq)}} + {{\text{H}}^ + }{\text{(aq)}} \rightleftharpoons {\text{H}}{{\text{S}}_2}{\text{O}}_3^ - {\text{(aq)}}\) Fast
\({\text{H}}{{\text{S}}_2}{\text{O}}_3^ - {\text{(aq)}} + {{\text{H}}^ + }{\text{(aq)}} \to {\text{S}}{{\text{O}}_2}{\text{(g)}} + {\text{S(s)}} + {{\text{H}}_2}{\text{O(l)}}\) Slow
The teacher asked the students to devise another technique to measure the rate of this reaction.
Another group suggested collecting the sulfur dioxide and drawing a graph of the volume of gas against time.
(i) State the volumes of the liquids that should be mixed.

(ii) State why it is important that the students use a similar beaker for both reactions.
(iii) If the reaction were first order with respect to the thiosulfate ion, predict the time it would take for the mark on the paper to be obscured when the concentration of sodium thiosulfate solution is halved.
(i) Deduce the rate expression of this mechanism.
(ii) The results of an experiment investigating the effect of the concentration of hydrochloric acid on the rate, while keeping the concentration of thiosulfate at the original value, are given in the table below.

On the axes provided, draw an appropriate graph to investigate the order of the reaction with respect to hydrochloric acid.
(iii) Identify two ways in which these data do not support the rate expression deduced in part (i).
(i) Sketch and label, indicating an approximate activation energy, the Maxwell–Boltzmann energy distribution curves for two temperatures, \({T_1}\) and \(T2{\text{ }}({T_2} > {T_1})\), at which the rate of reaction would be significantly different.

(ii) Explain why increasing the temperature of the reaction mixture would significantly increase the rate of the reaction.
(i) One group suggested recording how long it takes for the pH of the solution to change by one unit. Calculate the initial pH of the original reaction mixture.
(ii) Deduce the percentage of hydrochloric acid that would have to be used up for the pH to change by one unit.
Calculate the volume of sulfur dioxide, in \({\text{c}}{{\text{m}}^{\text{3}}}\), that the original reaction mixture would produce if it were collected at \(1.00 \times {10^5}{\text{ Pa}}\) and 300 K.
Sulfur dioxide, a major cause of acid rain, is quite soluble in water and the equilibrium shown below is established.
\({\text{S}}{{\text{O}}_2}{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{HSO}}_3^ - {\text{(aq)}} + {{\text{H}}^ + }{\text{(aq)}}\)
Given that the \({K_{\text{a}}}\) for this equilibrium is \(1.25 \times {10^{ - 2}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\), determine the pH of a \(2.00{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of sulfur dioxide.
Using Table 15 of the Data Booklet, identify an organic acid that is a stronger acid than sulfur dioxide.
Markscheme
(i)  ;
;
Accept other volumes in a 1:2:2 ratio.
(ii) depth of liquid in the beaker must remain constant / OWTTE;
Accept “same thickness of glass” and any other valid point, such as answers framed around minimizing uncontrolled variables / making it a “fair test”.
(iii) 94 (s) / 1 min 34 s;
(i) \({\text{rate}} = k{\text{[}}{{\text{S}}_{\text{2}}}{\text{O}}_3^{2 - }{\text{][}}{{\text{H}}^ + }{{\text{]}}^2}/{\text{rate}} = k{\text{[N}}{{\text{a}}_2}{{\text{S}}_2}{{\text{O}}_3}{\text{][HCl}}{{\text{]}}^2}\);
(ii) 
correct scale and units on y-axis;
Accept other suitable scales (such as 1/t) and units (such as ms–1).
Axes do not have to show origin/start at zero.
correct calculation of rate in \({s^{ - 1}}\);

If graph correct, assume this has been done on calculator and not written down.
correct plotting of points that the student decides to use and a connecting line;
Award final mark if 3 or more points are correct, irrespective of what is plotted on y-axis.
If line goes through the correct values at given concentrations of HCl, assume that points are marked there.
(iii) linear dependence on [HCl] (so not second order in \({\text{[}}{{\text{H}}^ + }{\text{]}}\));
Accept that doubling of concentration does not result in quadrupling of rate / OWTTE.
does not go through origin;
Remember to allow ECF from (b) (i).
(i) 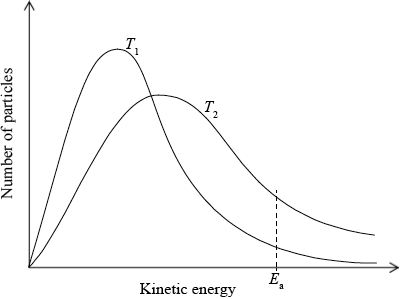
labelled y-axis: number of particles / probability of particles (with that kinetic energy) and labelled x-axis: (kinetic) energy;
Allow fraction/proportion/amount of particles (with kinetic energy) for y-axis label.
Allow speed/velocity for x-axis label.
\({T_2}\) curve broader and with maximum lower and to right of \({T_1}\) curve;
Do not award this mark if both curves not asymmetric.
Curves must pass through the origin and be asymptotic to x axis.
Do not award this mark if curves not labelled.
\({E_{\text{a}}}\) marked on graph;
(ii) kinetic energy of molecules increases;
This may be answered implicitly in the final marking point.
frequency of collision/number of collisions per unit time increases;
Do not accept “number of collisions increases”.
greater proportion of molecules have energy greater than/equal to activation energy / rate related to temperature by the Arrhenius equation;
Award [1 max] for statements such as “there will be more successful collisions” if neither of last two marking points awarded.
(i) \({\text{[}}{{\text{H}}^ + }{\text{]}} = 0.5 \times \frac{{10}}{{50}} = 0.1{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({\text{pH (}} = - \log {\text{[H}}{{\text{r}}^ + }{\text{]}} = - \log (0.10)) = 1\);
(ii) 90%;
\({\text{mol N}}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}} = {\text{mol S}}{{\text{O}}_{\text{2}}} = 0.0400 \times 0.0200 = 0.000800\);
\(V = \frac{{n \times R \times T}}{p}/\frac{{0.000800 \times 8.31 \times 300}}{{{{10}^5}}}\);
\((1.99 \times {10^{ - 5}}{\text{ }}{{\text{m}}^3}) = 19.9{\text{ }}({\text{c}}{{\text{m}}^3})\);
Note that two errors involving a factor of 1000 can also produce the correct answer. If this is the case award [1] not [3].
Accept 20.0 cm3 if R =8.314 is used.
Award [2] for 17.9 cm3 or 19.2 cm3 (result from using molar volume at standard temperature and pressure or at room temperature and pressure).
OR
\({\text{mol N}}{{\text{a}}_2}{{\text{S}}_2}{{\text{O}}_3} = {\text{mol S}}{{\text{O}}_2} = 0.0400 \times 0.0200 = 0.000800\);
\(V = 0.00080 \times 2.24 \times {10^{ - 2}} \times \left[ {\frac{{1.00 \times {{10}^5}}}{{1.01 \times {{10}^5}}}} \right] \times \frac{{300}}{{273}}\);
\((1.95 \times {10^{ - 5}}{\text{ }}{{\text{m}}^3}) = 19.5{\text{ }}({\text{c}}{{\text{m}}^3})\);
Note that two errors involving a factor of 1000 can also produce the correct answer. If this is the case award [1] not [3].
Deduct [1] for answers based on amount of HCl, so correct calculation would score [2 max].
\({K_{\text{a}}} = \frac{{{\text{[}}{{\text{H}}^ + }{\text{][HSO}}_3^ - {\text{]}}}}{{{\text{[}}{{\text{H}}_2}{\text{S}}{{\text{O}}_3}{\text{]}}}} = \frac{{{x^2}}}{{2 - x}} \approx \frac{{{x^2}}}{2} \approx 1.25 \times {10^{ - 2}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({\text{[}}{{\text{H}}^ + }{\text{]}} = \sqrt {2.50 \times {{10}^{ - 2}}} = 0.158{\text{ }}({\text{mol}}\,{\text{d}}{{\text{m}}^{ - 3}})\);
\({\text{pH}} = - \log (0.158) = 0.80\);
Award [3] for correct final answer.
dichloroethanoic acid / trichloroethanoic acid / 2,4,6-trinitrophenol;
Examiners report
This was quite a popular question, though generally not well answered. In the first part students again appeared to display a lack of expertise in a practical context with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and answers predicting that this would halve the reaction time were far more commonly encountered than those doubling it. Many candidates did however suggest valid reasons why the reaction vessel should remain unchanged and a significant number of students were able to correctly deduce the rate equation that the mechanism given would predict. Again a lack of ability to interpret experimental data was evident in the fact that it was very rare to find students who realised that a graph of (time)-1 against concentration was required to be able to deduce the reaction order, with almost all simply plotting time-concentration graphs and, as a result, very few could evaluate the mechanism in the light of the experimental data. Part (c) was a fairly standard question on the effect of temperature on reaction rate, hence it was a surprise that students did not score better on it, with many of the oft repeated mistakes (number of collisions rather than collision frequency) again coming to the surface. Again it was probably inability to interpret experimental data that led to only very few students being able to correctly state the initial pH of the mixture (I am certain almost all would have gained the mark if the pH of \({\text{ 0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl had been asked for) and the percentage that would have to be consumed to increase the pH by one unit (which is independent of the previous answer) proved too much for almost all candidates. In part (e) most students could quote and substitute into the ideal gas equation, but converting from \({{\text{m}}^3}\) to \({\text{c}}{{\text{m}}^3}\) posed a problem for most candidates. Quite a number of candidates were however able to calculate the pH of the sulfur dioxide solution and identify a stronger acid.
This was quite a popular question, though generally not well answered. In the first part students again appeared to display a lack of expertise in a practical context with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and answers predicting that this would halve the reaction time were far more commonly encountered than those doubling it. Many candidates did however suggest valid reasons why the reaction vessel should remain unchanged and a significant number of students were able to correctly deduce the rate equation that the mechanism given would predict. Again a lack of ability to interpret experimental data was evident in the fact that it was very rare to find students who realised that a graph of (time)-1 against concentration was required to be able to deduce the reaction order, with almost all simply plotting time-concentration graphs and, as a result, very few could evaluate the mechanism in the light of the experimental data. Part (c) was a fairly standard question on the effect of temperature on reaction rate, hence it was a surprise that students did not score better on it, with many of the oft repeated mistakes (number of collisions rather than collision frequency) again coming to the surface. Again it was probably inability to interpret experimental data that led to only very few students being able to correctly state the initial pH of the mixture (I am certain almost all would have gained the mark if the pH of \({\text{ 0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl had been asked for) and the percentage that would have to be consumed to increase the pH by one unit (which is independent of the previous answer) proved too much for almost all candidates. In part (e) most students could quote and substitute into the ideal gas equation, but converting from \({{\text{m}}^3}\) to \({\text{c}}{{\text{m}}^3}\) posed a problem for most candidates. Quite a number of candidates were however able to calculate the pH of the sulfur dioxide solution and identify a stronger acid.
This was quite a popular question, though generally not well answered. In the first part students again appeared to display a lack of expertise in a practical context with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and answers predicting that this would halve the reaction time were far more commonly encountered than those doubling it. Many candidates did however suggest valid reasons why the reaction vessel should remain unchanged and a significant number of students were able to correctly deduce the rate equation that the mechanism given would predict. Again a lack of ability to interpret experimental data was evident in the fact that it was very rare to find students who realised that a graph of (time)-1 against concentration was required to be able to deduce the reaction order, with almost all simply plotting time-concentration graphs and, as a result, very few could evaluate the mechanism in the light of the experimental data. Part (c) was a fairly standard question on the effect of temperature on reaction rate, hence it was a surprise that students did not score better on it, with many of the oft repeated mistakes (number of collisions rather than collision frequency) again coming to the surface. Again it was probably inability to interpret experimental data that led to only very few students being able to correctly state the initial pH of the mixture (I am certain almost all would have gained the mark if the pH of \({\text{ 0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl had been asked for) and the percentage that would have to be consumed to increase the pH by one unit (which is independent of the previous answer) proved too much for almost all candidates. In part (e) most students could quote and substitute into the ideal gas equation, but converting from \({{\text{m}}^3}\) to \({\text{c}}{{\text{m}}^3}\) posed a problem for most candidates. Quite a number of candidates were however able to calculate the pH of the sulfur dioxide solution and identify a stronger acid.
This was quite a popular question, though generally not well answered. In the first part students again appeared to display a lack of expertise in a practical context with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and answers predicting that this would halve the reaction time were far more commonly encountered than those doubling it. Many candidates did however suggest valid reasons why the reaction vessel should remain unchanged and a significant number of students were able to correctly deduce the rate equation that the mechanism given would predict. Again a lack of ability to interpret experimental data was evident in the fact that it was very rare to find students who realised that a graph of (time)-1 against concentration was required to be able to deduce the reaction order, with almost all simply plotting time-concentration graphs and, as a result, very few could evaluate the mechanism in the light of the experimental data. Part (c) was a fairly standard question on the effect of temperature on reaction rate, hence it was a surprise that students did not score better on it, with many of the oft repeated mistakes (number of collisions rather than collision frequency) again coming to the surface. Again it was probably inability to interpret experimental data that led to only very few students being able to correctly state the initial pH of the mixture (I am certain almost all would have gained the mark if the pH of \({\text{ 0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl had been asked for) and the percentage that would have to be consumed to increase the pH by one unit (which is independent of the previous answer) proved too much for almost all candidates. In part (e) most students could quote and substitute into the ideal gas equation, but converting from \({{\text{m}}^3}\) to \({\text{c}}{{\text{m}}^3}\) posed a problem for most candidates. Quite a number of candidates were however able to calculate the pH of the sulfur dioxide solution and identify a stronger acid.
This was quite a popular question, though generally not well answered. In the first part students again appeared to display a lack of expertise in a practical context with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and answers predicting that this would halve the reaction time were far more commonly encountered than those doubling it. Many candidates did however suggest valid reasons why the reaction vessel should remain unchanged and a significant number of students were able to correctly deduce the rate equation that the mechanism given would predict. Again a lack of ability to interpret experimental data was evident in the fact that it was very rare to find students who realised that a graph of (time)-1 against concentration was required to be able to deduce the reaction order, with almost all simply plotting time-concentration graphs and, as a result, very few could evaluate the mechanism in the light of the experimental data. Part (c) was a fairly standard question on the effect of temperature on reaction rate, hence it was a surprise that students did not score better on it, with many of the oft repeated mistakes (number of collisions rather than collision frequency) again coming to the surface. Again it was probably inability to interpret experimental data that led to only very few students being able to correctly state the initial pH of the mixture (I am certain almost all would have gained the mark if the pH of \({\text{ 0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl had been asked for) and the percentage that would have to be consumed to increase the pH by one unit (which is independent of the previous answer) proved too much for almost all candidates. In part (e) most students could quote and substitute into the ideal gas equation, but converting from \({{\text{m}}^3}\) to \({\text{c}}{{\text{m}}^3}\) posed a problem for most candidates. Quite a number of candidates were however able to calculate the pH of the sulfur dioxide solution and identify a stronger acid.
This was quite a popular question, though generally not well answered. In the first part students again appeared to display a lack of expertise in a practical context with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and answers predicting that this would halve the reaction time were far more commonly encountered than those doubling it. Many candidates did however suggest valid reasons why the reaction vessel should remain unchanged and a significant number of students were able to correctly deduce the rate equation that the mechanism given would predict. Again a lack of ability to interpret experimental data was evident in the fact that it was very rare to find students who realised that a graph of (time)-1 against concentration was required to be able to deduce the reaction order, with almost all simply plotting time-concentration graphs and, as a result, very few could evaluate the mechanism in the light of the experimental data. Part (c) was a fairly standard question on the effect of temperature on reaction rate, hence it was a surprise that students did not score better on it, with many of the oft repeated mistakes (number of collisions rather than collision frequency) again coming to the surface. Again it was probably inability to interpret experimental data that led to only very few students being able to correctly state the initial pH of the mixture (I am certain almost all would have gained the mark if the pH of \({\text{ 0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl had been asked for) and the percentage that would have to be consumed to increase the pH by one unit (which is independent of the previous answer) proved too much for almost all candidates. In part (e) most students could quote and substitute into the ideal gas equation, but converting from \({{\text{m}}^3}\) to \({\text{c}}{{\text{m}}^3}\) posed a problem for most candidates. Quite a number of candidates were however able to calculate the pH of the sulfur dioxide solution and identify a stronger acid.
This was quite a popular question, though generally not well answered. In the first part students again appeared to display a lack of expertise in a practical context with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and answers predicting that this would halve the reaction time were far more commonly encountered than those doubling it. Many candidates did however suggest valid reasons why the reaction vessel should remain unchanged and a significant number of students were able to correctly deduce the rate equation that the mechanism given would predict. Again a lack of ability to interpret experimental data was evident in the fact that it was very rare to find students who realised that a graph of (time)-1 against concentration was required to be able to deduce the reaction order, with almost all simply plotting time-concentration graphs and, as a result, very few could evaluate the mechanism in the light of the experimental data. Part (c) was a fairly standard question on the effect of temperature on reaction rate, hence it was a surprise that students did not score better on it, with many of the oft repeated mistakes (number of collisions rather than collision frequency) again coming to the surface. Again it was probably inability to interpret experimental data that led to only very few students being able to correctly state the initial pH of the mixture (I am certain almost all would have gained the mark if the pH of \({\text{ 0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl had been asked for) and the percentage that would have to be consumed to increase the pH by one unit (which is independent of the previous answer) proved too much for almost all candidates. In part (e) most students could quote and substitute into the ideal gas equation, but converting from \({{\text{m}}^3}\) to \({\text{c}}{{\text{m}}^3}\) posed a problem for most candidates. Quite a number of candidates were however able to calculate the pH of the sulfur dioxide solution and identify a stronger acid.
Iron tablets are often prescribed to patients. The iron in the tablets is commonly present as iron(II) sulfate, FeSO4.
Following the experiment, the students proposed the following hypothesis:
“Since sulfuric acid is a strong acid, two other strong acids such as nitric acid, HNO3(aq) or hydrochloric acid, HCl(aq), could also be used in this experiment”.
Suggest one problem with this hypothesis.
The students also explored the role of sulfuric acid in everyday processes and found that sulfuric acid present in acid rain can damage buildings made of limestone. Predict the balanced chemical equation for the reaction between limestone and sulfuric acid, including state symbols.
Markscheme
\({\text{NO}}_{\text{3}}^ - \) and \({\text{C}}{{\text{l}}^ - }\) anions may also react with \({\text{KMn}}{{\text{O}}_{\text{4}}}\) / \({\text{HN}}{{\text{O}}_{\text{3}}}\) is an oxidizing agent / (HCl will not work as) \({\text{C}}{{\text{l}}^ - }\) reacts with \({\text{MnO}}_{\text{4}}^ - \) (to form \({\text{C}}{{\text{l}}_{\text{2}}}\)) / HCl oxidized / OWTTE;
For HCl, allow correctly balanced chemical equation:
2MnO4–+10Cl–+16H+\( \to \)2Mn2++5Cl2+8H2O
Accept NO3– and Cl– may react with KMnO4/Fe2+.
\({\text{CaC}}{{\text{O}}_3}{\text{(s)}} + {{\text{H}}_2}{\text{S}}{{\text{O}}_4}{\text{(aq)}} \to {\text{CaS}}{{\text{O}}_4}{\text{(s)}} + {{\text{H}}_2}{\text{O(l)}} + {\text{C}}{{\text{O}}_2}{\text{(g)}}\)
correct chemical equation;
correct state symbols;
Allow CaSO4(aq) instead of CaSO4(s).
M2 can only be scored if M1 is correct.
Award [1max] if H2CO3(aq) is given instead of H2O(l) + CO2(g).
Examiners report
Most candidates were able to state the function of iron in the body but unable to explain why a reading of the top meniscus is taken for the KMnO4 titration, which suggests limited practical experience. Some candidates calculated the moles of Fe using the mass of tablets rather than using mole ratio and titre results. most candidates were able to define ‘reduction’ and determine the oxidation number, although some were penalized for incorrect notation. Many did not know how to prevent the formation of MnO2 precipitate or why HCl or HNO3 are not used in this titration.
Most candidates were able to state the function of iron in the body but unable to explain why a reading of the top meniscus is taken for the KMnO4 titration, which suggests limited practical experience. Some candidates calculated the moles of Fe using the mass of tablets rather than using mole ratio and titre results. most candidates were able to define ‘reduction’ and determine the oxidation number, although some were penalized for incorrect notation. Many did not know how to prevent the formation of MnO2 precipitate or why HCl or HNO3 are not used in this titration.
Calcium nitrate contains both covalent and ionic bonds.
Nitrogen also forms oxides, which are atmospheric pollutants.
State the formula of both ions present and the nature of the force between these ions.
Ions:
Nature of force:
State which atoms are covalently bonded.
Bonding in the nitrate ion involves electron delocalization. Explain the meaning of electron delocalization and how it affects the ion.
Outline the source of these oxides.
State one product formed from their reaction with water.
State one environmental problem caused by these atmospheric pollutants.
Markscheme
\({\text{C}}{{\text{a}}^{2 + }}\) and \({\text{NO}}_3^ - \);
electrostatic (attraction);
Do not accept ionic.
nitrogen/N and oxygen/O;
Do not accept nitrate/NO3–.
Accept atoms in nitrate/NO3–
pi/\(\underline \pi \)-electrons shared by more than two atoms/nuclei / a pi/\(\underline \pi \)-bond/overlapping p-orbitals that extends over more than two atoms/nuclei;
all (N–O) bonds equal length/strength/bond-order / charge on all oxygen/O atoms equal / increases stability/lowers PE (of the ion);
Accept a diagram that clearly shows one or both points.
produced by high temperature combustion;
Accept combustion/jet/car engines / car exhaust/emissions / lightning / action of bacteria/microorganisms.
Do not accept combustion/burning, cars, planes, jets, factories, power plants etc.
nitric acid/\({\text{HN}}{{\text{O}}_{\text{3}}}\) / nitrous acid/nitric(III) acid/\({\text{HN}}{{\text{O}}_{\text{2}}}\);
Accept “form acidic solutions / acid rain”.
acid deposition/rain / respiratory problems / corrosion problems / decomposition of ozone layer / photochemical smog / acidification/pollution of lakes / damage to plants/ trees;
Accept “acid rain” in either part (ii) or part (iii) but not both.
Do not accept air pollution.
Examiners report
It was distressing how many students taking HL Chemistry (over 50%?) do not know the formula of the nitrate ion! Many students also gave the type of bonding present between the ions, rather than the nature of the force asked for, though almost all could correctly identify the covalently bonded atoms. Hardly any could explain delocalization in terms of the overlap of p-orbitals, or the extension of a \(\pi \)-bond, over more than two atoms, though its effect on structure and stability were better known. In part (c), which tested Aim 8 of the syllabus, most managed to gain some of the marks available for atmospheric pollution from oxides of nitrogen. Inevitably, owing to some overlap in assessment statements these concepts would be more familiar to those studying the Environmental Chemistry option, but undoubtedly studying other options assists in other areas, such as organic chemistry.
It was distressing how many students taking HL Chemistry (over 50%?) do not know the formula of the nitrate ion! Many students also gave the type of bonding present between the ions, rather than the nature of the force asked for, though almost all could correctly identify the covalently bonded atoms. Hardly any could explain delocalization in terms of the overlap of p-orbitals, or the extension of a \(\pi \)-bond, over more than two atoms, though its effect on structure and stability were better known. In part (c), which tested Aim 8 of the syllabus, most managed to gain some of the marks available for atmospheric pollution from oxides of nitrogen. Inevitably, owing to some overlap in assessment statements these concepts would be more familiar to those studying the Environmental Chemistry option, but undoubtedly studying other options assists in other areas, such as organic chemistry.
It was distressing how many students taking HL Chemistry (over 50%?) do not know the formula of the nitrate ion! Many students also gave the type of bonding present between the ions, rather than the nature of the force asked for, though almost all could correctly identify the covalently bonded atoms. Hardly any could explain delocalization in terms of the overlap of p-orbitals, or the extension of a \(\pi \)-bond, over more than two atoms, though its effect on structure and stability were better known. In part (c), which tested Aim 8 of the syllabus, most managed to gain some of the marks available for atmospheric pollution from oxides of nitrogen. Inevitably, owing to some overlap in assessment statements these concepts would be more familiar to those studying the Environmental Chemistry option, but undoubtedly studying other options assists in other areas, such as organic chemistry.
It was distressing how many students taking HL Chemistry (over 50%?) do not know the formula of the nitrate ion! Many students also gave the type of bonding present between the ions, rather than the nature of the force asked for, though almost all could correctly identify the covalently bonded atoms. Hardly any could explain delocalization in terms of the overlap of p-orbitals, or the extension of a \(\pi \)-bond, over more than two atoms, though its effect on structure and stability were better known. In part (c), which tested Aim 8 of the syllabus, most managed to gain some of the marks available for atmospheric pollution from oxides of nitrogen. Inevitably, owing to some overlap in assessment statements these concepts would be more familiar to those studying the Environmental Chemistry option, but undoubtedly studying other options assists in other areas, such as organic chemistry.
It was distressing how many students taking HL Chemistry (over 50%?) do not know the formula of the nitrate ion! Many students also gave the type of bonding present between the ions, rather than the nature of the force asked for, though almost all could correctly identify the covalently bonded atoms. Hardly any could explain delocalization in terms of the overlap of p-orbitals, or the extension of a \(\pi \)-bond, over more than two atoms, though its effect on structure and stability were better known. In part (c), which tested Aim 8 of the syllabus, most managed to gain some of the marks available for atmospheric pollution from oxides of nitrogen. Inevitably, owing to some overlap in assessment statements these concepts would be more familiar to those studying the Environmental Chemistry option, but undoubtedly studying other options assists in other areas, such as organic chemistry.
It was distressing how many students taking HL Chemistry (over 50%?) do not know the formula of the nitrate ion! Many students also gave the type of bonding present between the ions, rather than the nature of the force asked for, though almost all could correctly identify the covalently bonded atoms. Hardly any could explain delocalization in terms of the overlap of p-orbitals, or the extension of a \(\pi \)-bond, over more than two atoms, though its effect on structure and stability were better known. In part (c), which tested Aim 8 of the syllabus, most managed to gain some of the marks available for atmospheric pollution from oxides of nitrogen. Inevitably, owing to some overlap in assessment statements these concepts would be more familiar to those studying the Environmental Chemistry option, but undoubtedly studying other options assists in other areas, such as organic chemistry.
In acidic solution, ions containing titanium can react according to the half-equation below.
\({\text{Ti}}{{\text{O}}^{2 + }}{\text{(aq)}} + {\text{2}}{{\text{H}}^ + }{\text{(aq)}} + {{\text{e}}^ - } \rightleftharpoons {\text{T}}{{\text{i}}^{3 + }}{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}}\) \({E^\Theta } = - 0.06{\text{ V}}\)
In the diagram below, A and B are inert electrodes and, in the aqueous solutions, all ions have a concentration of \({\text{1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\).
Sodium, silicon and sulfur are elements in period 3 of the periodic table that all form oxides.
Although carbon and silicon both belong to group 4 of the periodic table, carbon dioxide and silicon dioxide are different in many ways.
Define the term standard electrode potential, \({E^\Theta }\).
State the initial and final oxidation numbers of titanium and hence deduce whether it is oxidized or reduced in this change.

Considering the above equilibrium, predict, giving a reason, how adding more acid would affect the strength of the \({\text{Ti}}{{\text{O}}^{2 + }}\) ion as an oxidizing agent.
In the two experiments below, predict whether a reaction would occur and deduce an equation for any reaction that takes place. Refer to Table 14 of the Data Booklet if necessary.
KI(aq) is added to a solution containing \({\text{T}}{{\text{i}}^{3 + }}{\text{(aq)}}\) ions:
Zn (s) is added to a solution containing \({\text{Ti}}{{\text{O}}^{2 + }}{\text{(aq)}}\) and \({{\text{H}}^ + }{\text{(aq)}}\) ions:
Using Table 14 of the Data Booklet, state the balanced half-equation for the reaction that occurs at electrode A and whether it involves oxidation or reduction.
Calculate the cell potential in V.
On the diagram above label with an arrow
• the direction of electron flow in the wire
• the direction in which the positive ions flow in the salt bridge.
Compare the properties of the three oxides by completing the table below.
Sulfur dioxide is a significant contributor to acid deposition. Identify a major, man-made source of this pollutant.
As well as the oxide above, sodium forms a peroxide that contains the peroxide ion, \({\text{O}}_2^{2 - }\). Draw the Lewis (electron dot) structure of the peroxide ion.
Describe the differences in the hybridization of these group 4 elements and the precise nature of the bonds that they form with the oxygen atoms.
Xenon, although a noble gas, forms an oxide, \({\text{Xe}}{{\text{O}}_{\text{2}}}\), that has a structure related to that of \({\text{Si}}{{\text{O}}_{\text{2}}}\). Compare the geometry around the silicon atoms in \({\text{Si}}{{\text{O}}_{\text{2}}}\) with the geometry around the xenon atoms in \({\text{Xe}}{{\text{O}}_{\text{2}}}\), using the valence shell electron pair repulsion (VSEPR) theory.
Markscheme
potential of the half-cell / reduction half-reaction under standard conditions measured relative to standard hydrogen electrode/SHE;
Allow instead of standard conditions, solute concentration of 1 mol dm–3 or 1 bar/1 atm (pressure) for gases.

+ sign must be present. Do not award mark for incorrect notation 4, 4+, 3, 3+ etc.
Do not award M2 if inconsistent with M1.
increases / makes it stronger;
(more \({{\text{H}}^ + }\) would) drive/shift equilibrium to the right/towards products (accepting more electrons);
KI(aq) is added to a solution containing Ti3+(aq) ions:
no reaction;
Zn(s) is added to a solution containing TiO2+(aq) and H+(aq) ions:
\({\text{Zn(s)}} + {\text{2Ti}}{{\text{O}}^{2 + }}{\text{(aq)}} + {\text{4}}{{\text{H}}^ + }{\text{(aq)}} \to {\text{Z}}{{\text{n}}^{2 + }}{\text{(aq)}} + {\text{2T}}{{\text{i}}^{3 + }}{\text{(aq)}} + {\text{2}}{{\text{H}}_2}{\text{O(l)}}\)
correct reactants and products;
balanced equation;
Ignore state symbols.
\({\text{F}}{{\text{e}}^{3 + }}{\text{(aq)}} + {{\text{e}}^ - } \to {\text{F}}{{\text{e}}^{2 + }}{\text{(aq)}}\);
Ignore state symbols.
Accept equilibrium arrow.
reduction;
Do not apply ECF.
\(( + 0.77 - ( - 0.06)) = ( + )0.83{\text{ (V)}}\);
Do not accept –0.83 V.
wire and salt bridge both have arrows from B to A;
Accept arrows above or below each provided it is obvious which they refer to.
Apply ECF from part (i).
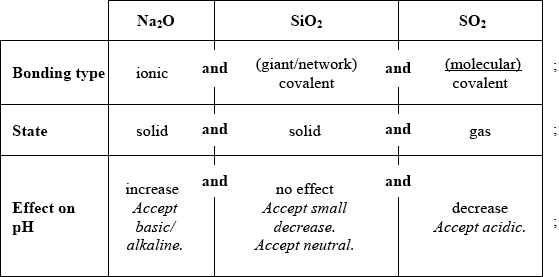
For any parts (properties) where mark not awarded, award [1] for every three correct responses.
(combustion of) coal / diesel;
Accept “burning of fossil fuels”, “industrial processes” or “combustion/car engines”.
Do not accept “Contact process”.

e-pairs correct;
charges in correct positions;
Accept lines, or pairs of dots or crosses, for electron pairs.
Accept 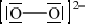 .
.
C is sp hybridized and Si is \({\text{s}}{{\text{p}}^{\text{3}}}\) hybridized;
C–O bond in \({\text{C}}{{\text{O}}_{\text{2}}}\) has one \(\sigma \)-bond and one \(\pi \)-bond;
Si–O bond in \({\text{Si}}{{\text{O}}_{\text{2}}}\) has one \(\sigma \)-bond only;
Award [1 max] for last two marking points for “C–O double bond and Si–O single bond”.
silicon-oxygen bonds will have a tetrahedral distribution;
xenon-oxygen bonds will have a square planar distribution;
xenon dioxide has two non-bonding/lone pairs of electrons;
Award any of the above marks if clearly indicated in suitable diagrams.
Examiners report
The required definition and the effect of acid on the oxidizing power of \({\text{Ti}}{{\text{O}}^{2 + }}\) was often well done, though it proved a challenge for some candidates, and most could interpret the change in terms of oxidation numbers. Very few candidates could use \({E^\Theta }\) values to predict whether a reaction with another half-cell would occur and even less could correctly combine the half-equations to produce a balanced equation for the overall reaction. Relatively few candidates managed to gain full marks for the questions relating to the voltaic cell illustrated, with the different parts appearing to be of approximately equal difficulty. The nature of the period 3 oxides was generally well appreciated, though often the effect on pH was expressed as, for example, “basic” rather than “increases”. In spite of the efficiency of modern plants many considered the contact process to be a major source of sulfur dioxide pollution, rather than combustion of coal and other “high sulfur” fossil fuels. The comparison of the structure of silicon dioxide to those of carbon and xenon dioxides was poorly done, the root cause often being a lack of awareness of the structure of silicon dioxide. Many candidates could however write correct equations for the reaction of silicon tetrachloride with water.
The required definition and the effect of acid on the oxidizing power of \({\text{Ti}}{{\text{O}}^{2 + }}\) was often well done, though it proved a challenge for some candidates, and most could interpret the change in terms of oxidation numbers. Very few candidates could use \({E^\Theta }\) values to predict whether a reaction with another half-cell would occur and even less could correctly combine the half-equations to produce a balanced equation for the overall reaction. Relatively few candidates managed to gain full marks for the questions relating to the voltaic cell illustrated, with the different parts appearing to be of approximately equal difficulty. The nature of the period 3 oxides was generally well appreciated, though often the effect on pH was expressed as, for example, “basic” rather than “increases”. In spite of the efficiency of modern plants many considered the contact process to be a major source of sulfur dioxide pollution, rather than combustion of coal and other “high sulfur” fossil fuels. The comparison of the structure of silicon dioxide to those of carbon and xenon dioxides was poorly done, the root cause often being a lack of awareness of the structure of silicon dioxide. Many candidates could however write correct equations for the reaction of silicon tetrachloride with water.
The required definition and the effect of acid on the oxidizing power of \({\text{Ti}}{{\text{O}}^{2 + }}\) was often well done, though it proved a challenge for some candidates, and most could interpret the change in terms of oxidation numbers. Very few candidates could use \({E^\Theta }\) values to predict whether a reaction with another half-cell would occur and even less could correctly combine the half-equations to produce a balanced equation for the overall reaction. Relatively few candidates managed to gain full marks for the questions relating to the voltaic cell illustrated, with the different parts appearing to be of approximately equal difficulty. The nature of the period 3 oxides was generally well appreciated, though often the effect on pH was expressed as, for example, “basic” rather than “increases”. In spite of the efficiency of modern plants many considered the contact process to be a major source of sulfur dioxide pollution, rather than combustion of coal and other “high sulfur” fossil fuels. The comparison of the structure of silicon dioxide to those of carbon and xenon dioxides was poorly done, the root cause often being a lack of awareness of the structure of silicon dioxide. Many candidates could however write correct equations for the reaction of silicon tetrachloride with water.
The required definition and the effect of acid on the oxidizing power of \({\text{Ti}}{{\text{O}}^{2 + }}\) was often well done, though it proved a challenge for some candidates, and most could interpret the change in terms of oxidation numbers. Very few candidates could use \({E^\Theta }\) values to predict whether a reaction with another half-cell would occur and even less could correctly combine the half-equations to produce a balanced equation for the overall reaction. Relatively few candidates managed to gain full marks for the questions relating to the voltaic cell illustrated, with the different parts appearing to be of approximately equal difficulty. The nature of the period 3 oxides was generally well appreciated, though often the effect on pH was expressed as, for example, “basic” rather than “increases”. In spite of the efficiency of modern plants many considered the contact process to be a major source of sulfur dioxide pollution, rather than combustion of coal and other “high sulfur” fossil fuels. The comparison of the structure of silicon dioxide to those of carbon and xenon dioxides was poorly done, the root cause often being a lack of awareness of the structure of silicon dioxide. Many candidates could however write correct equations for the reaction of silicon tetrachloride with water.
The required definition and the effect of acid on the oxidizing power of \({\text{Ti}}{{\text{O}}^{2 + }}\) was often well done, though it proved a challenge for some candidates, and most could interpret the change in terms of oxidation numbers. Very few candidates could use \({E^\Theta }\) values to predict whether a reaction with another half-cell would occur and even less could correctly combine the half-equations to produce a balanced equation for the overall reaction. Relatively few candidates managed to gain full marks for the questions relating to the voltaic cell illustrated, with the different parts appearing to be of approximately equal difficulty. The nature of the period 3 oxides was generally well appreciated, though often the effect on pH was expressed as, for example, “basic” rather than “increases”. In spite of the efficiency of modern plants many considered the contact process to be a major source of sulfur dioxide pollution, rather than combustion of coal and other “high sulfur” fossil fuels. The comparison of the structure of silicon dioxide to those of carbon and xenon dioxides was poorly done, the root cause often being a lack of awareness of the structure of silicon dioxide. Many candidates could however write correct equations for the reaction of silicon tetrachloride with water.
The required definition and the effect of acid on the oxidizing power of \({\text{Ti}}{{\text{O}}^{2 + }}\) was often well done, though it proved a challenge for some candidates, and most could interpret the change in terms of oxidation numbers. Very few candidates could use \({E^\Theta }\) values to predict whether a reaction with another half-cell would occur and even less could correctly combine the half-equations to produce a balanced equation for the overall reaction. Relatively few candidates managed to gain full marks for the questions relating to the voltaic cell illustrated, with the different parts appearing to be of approximately equal difficulty. The nature of the period 3 oxides was generally well appreciated, though often the effect on pH was expressed as, for example, “basic” rather than “increases”. In spite of the efficiency of modern plants many considered the contact process to be a major source of sulfur dioxide pollution, rather than combustion of coal and other “high sulfur” fossil fuels. The comparison of the structure of silicon dioxide to those of carbon and xenon dioxides was poorly done, the root cause often being a lack of awareness of the structure of silicon dioxide. Many candidates could however write correct equations for the reaction of silicon tetrachloride with water.
The required definition and the effect of acid on the oxidizing power of \({\text{Ti}}{{\text{O}}^{2 + }}\) was often well done, though it proved a challenge for some candidates, and most could interpret the change in terms of oxidation numbers. Very few candidates could use \({E^\Theta }\) values to predict whether a reaction with another half-cell would occur and even less could correctly combine the half-equations to produce a balanced equation for the overall reaction. Relatively few candidates managed to gain full marks for the questions relating to the voltaic cell illustrated, with the different parts appearing to be of approximately equal difficulty. The nature of the period 3 oxides was generally well appreciated, though often the effect on pH was expressed as, for example, “basic” rather than “increases”. In spite of the efficiency of modern plants many considered the contact process to be a major source of sulfur dioxide pollution, rather than combustion of coal and other “high sulfur” fossil fuels. The comparison of the structure of silicon dioxide to those of carbon and xenon dioxides was poorly done, the root cause often being a lack of awareness of the structure of silicon dioxide. Many candidates could however write correct equations for the reaction of silicon tetrachloride with water.
The required definition and the effect of acid on the oxidizing power of \({\text{Ti}}{{\text{O}}^{2 + }}\) was often well done, though it proved a challenge for some candidates, and most could interpret the change in terms of oxidation numbers. Very few candidates could use \({E^\Theta }\) values to predict whether a reaction with another half-cell would occur and even less could correctly combine the half-equations to produce a balanced equation for the overall reaction. Relatively few candidates managed to gain full marks for the questions relating to the voltaic cell illustrated, with the different parts appearing to be of approximately equal difficulty. The nature of the period 3 oxides was generally well appreciated, though often the effect on pH was expressed as, for example, “basic” rather than “increases”. In spite of the efficiency of modern plants many considered the contact process to be a major source of sulfur dioxide pollution, rather than combustion of coal and other “high sulfur” fossil fuels. The comparison of the structure of silicon dioxide to those of carbon and xenon dioxides was poorly done, the root cause often being a lack of awareness of the structure of silicon dioxide. Many candidates could however write correct equations for the reaction of silicon tetrachloride with water.
The required definition and the effect of acid on the oxidizing power of \({\text{Ti}}{{\text{O}}^{2 + }}\) was often well done, though it proved a challenge for some candidates, and most could interpret the change in terms of oxidation numbers. Very few candidates could use \({E^\Theta }\) values to predict whether a reaction with another half-cell would occur and even less could correctly combine the half-equations to produce a balanced equation for the overall reaction. Relatively few candidates managed to gain full marks for the questions relating to the voltaic cell illustrated, with the different parts appearing to be of approximately equal difficulty. The nature of the period 3 oxides was generally well appreciated, though often the effect on pH was expressed as, for example, “basic” rather than “increases”. In spite of the efficiency of modern plants many considered the contact process to be a major source of sulfur dioxide pollution, rather than combustion of coal and other “high sulfur” fossil fuels. The comparison of the structure of silicon dioxide to those of carbon and xenon dioxides was poorly done, the root cause often being a lack of awareness of the structure of silicon dioxide. Many candidates could however write correct equations for the reaction of silicon tetrachloride with water.
The required definition and the effect of acid on the oxidizing power of \({\text{Ti}}{{\text{O}}^{2 + }}\) was often well done, though it proved a challenge for some candidates, and most could interpret the change in terms of oxidation numbers. Very few candidates could use \({E^\Theta }\) values to predict whether a reaction with another half-cell would occur and even less could correctly combine the half-equations to produce a balanced equation for the overall reaction. Relatively few candidates managed to gain full marks for the questions relating to the voltaic cell illustrated, with the different parts appearing to be of approximately equal difficulty. The nature of the period 3 oxides was generally well appreciated, though often the effect on pH was expressed as, for example, “basic” rather than “increases”. In spite of the efficiency of modern plants many considered the contact process to be a major source of sulfur dioxide pollution, rather than combustion of coal and other “high sulfur” fossil fuels. The comparison of the structure of silicon dioxide to those of carbon and xenon dioxides was poorly done, the root cause often being a lack of awareness of the structure of silicon dioxide. Many candidates could however write correct equations for the reaction of silicon tetrachloride with water.
The required definition and the effect of acid on the oxidizing power of \({\text{Ti}}{{\text{O}}^{2 + }}\) was often well done, though it proved a challenge for some candidates, and most could interpret the change in terms of oxidation numbers. Very few candidates could use \({E^\Theta }\) values to predict whether a reaction with another half-cell would occur and even less could correctly combine the half-equations to produce a balanced equation for the overall reaction. Relatively few candidates managed to gain full marks for the questions relating to the voltaic cell illustrated, with the different parts appearing to be of approximately equal difficulty. The nature of the period 3 oxides was generally well appreciated, though often the effect on pH was expressed as, for example, “basic” rather than “increases”. In spite of the efficiency of modern plants many considered the contact process to be a major source of sulfur dioxide pollution, rather than combustion of coal and other “high sulfur” fossil fuels. The comparison of the structure of silicon dioxide to those of carbon and xenon dioxides was poorly done, the root cause often being a lack of awareness of the structure of silicon dioxide. Many candidates could however write correct equations for the reaction of silicon tetrachloride with water.
The required definition and the effect of acid on the oxidizing power of \({\text{Ti}}{{\text{O}}^{2 + }}\) was often well done, though it proved a challenge for some candidates, and most could interpret the change in terms of oxidation numbers. Very few candidates could use \({E^\Theta }\) values to predict whether a reaction with another half-cell would occur and even less could correctly combine the half-equations to produce a balanced equation for the overall reaction. Relatively few candidates managed to gain full marks for the questions relating to the voltaic cell illustrated, with the different parts appearing to be of approximately equal difficulty. The nature of the period 3 oxides was generally well appreciated, though often the effect on pH was expressed as, for example, “basic” rather than “increases”. In spite of the efficiency of modern plants many considered the contact process to be a major source of sulfur dioxide pollution, rather than combustion of coal and other “high sulfur” fossil fuels. The comparison of the structure of silicon dioxide to those of carbon and xenon dioxides was poorly done, the root cause often being a lack of awareness of the structure of silicon dioxide. Many candidates could however write correct equations for the reaction of silicon tetrachloride with water.
Oxidation and reduction can be defined in terms of electron transfer or oxidation numbers.
A reactivity series can be experimentally determined by adding the metals W, X, Y and Z to solutions of these metal ions. The following reactions were observed:
\({{\text{W}}^{2 + }}{\text{(aq)}} + {\text{X(s)}} \to {\text{W(s)}} + {{\text{X}}^{2 + }}{\text{(aq)}}\)
\({\text{Y(s)}} + {{\text{W}}^{2 + }}{\text{(aq)}} \to {{\text{Y}}^{2 + }}{\text{(aq)}} + {\text{W(s)}}\)
\({{\text{Z}}^{2 + }}{\text{(aq)}} + {\text{W(s)}} \to {\text{Z(s)}} + {{\text{W}}^{2 + }}{\text{(aq)}}\)
\({\text{Y(s)}} + {{\text{X}}^{2 + }}{\text{(aq)}} \to {{\text{Y}}^{2 + }}{\text{(aq)}} + {\text{X(s)}}\)
A student carries out the electrolysis of aqueous potassium iodide, KI, using inert electrodes.
Three electrolytic cells were set up in series (one cell after the other), as shown below.
All of the solutions had a concentration of \({\text{1.00 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\).
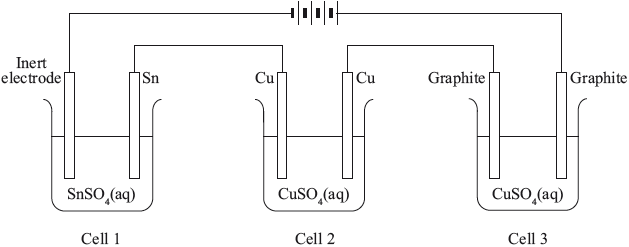
Alcohols with the molecular formula \({{\text{C}}_{\text{4}}}{{\text{H}}_{\text{9}}}{\text{OH}}\) occur as four structural isomers. Three of the isomers can be oxidized with acidified potassium dichromate solution to form compounds with the molecular formula \({{\text{C}}_{\text{4}}}{{\text{H}}_{\text{8}}}{\text{O}}\).
(i) Deduce the half-equation for the oxidation of the alcohol \({{\text{C}}_{\text{4}}}{{\text{H}}_{\text{9}}}{\text{OH}}\).
(ii) Deduce the overall equation for the redox reaction.
(iii) Two of the isomers with the molecular formula \({{\text{C}}_{\text{4}}}{{\text{H}}_{\text{9}}}{\text{OH}}\) can be oxidized further to form compounds with the molecular formula \({{\text{C}}_{\text{4}}}{{\text{H}}_{\text{8}}}{{\text{O}}_{\text{2}}}\). Deduce the structural formulas of these two isomers.
(iv) One isomer cannot be oxidized by acidified potassium dichromate solution.
Deduce its structural formula, state its name and identify it as a primary, secondary or tertiary alcohol.
Name:
Alcohol:
(v) All isomers of the alcohol \({{\text{C}}_{\text{4}}}{{\text{H}}_{\text{9}}}{\text{OH}}\) undergo complete combustion. State an equation for the complete combustion of \({{\text{C}}_{\text{4}}}{{\text{H}}_{\text{9}}}{\text{OH}}\).
(i) Deduce the order of reactivity of these four metals, from the least to the most reactive.
(ii) A voltaic cell is made by connecting a half-cell of X in \({\text{XC}}{{\text{l}}_{\text{2}}}{\text{(aq)}}\) to a half-cell of Z in \({\text{ZC}}{{\text{l}}_{\text{2}}}{\text{(aq)}}\). Deduce the overall equation for the reaction taking place when the cell is operating.
(iii) The standard electrode potential for \({{\text{Z}}^{2 + }}{\text{(aq)}} + {\text{2}}{{\text{e}}^ - } \rightleftharpoons {\text{Z(s)}}\) is \( + {\text{0.20 V}}\). State which species is oxidized when this half-cell is connected to a standard hydrogen electrode.
(iv) Describe the standard hydrogen electrode including a fully labelled diagram.
(i) State the half-equation for the reaction that occurs at each electrode.
Positive electrode (anode):
Negative electrode (cathode):
(ii) Suggest, giving a reason, what would happen if the electrodes were changed to aluminium.
(i) Determine the mass of copper produced at one of the electrodes in cell 2 if the tin electrode in cell 1 decreased in mass by 0.034 g.
(ii) Compare the colour and the pH of the solutions in cells 2 and 3 after the current has been flowing for one hour.
(iii) Explain your answer given for part (d) (ii).
Colour:
pH:
Markscheme
(i) \({{\text{C}}_4}{{\text{H}}_9}{\text{OH(l)}} \to {{\text{C}}_4}{{\text{H}}_8}{\text{O(l)}} + {\text{2}}{{\text{H}}^ + }{\text{(aq)}} + {\text{2}}{{\text{e}}^ - }\);
Ignore state symbols.
(ii) \({\text{3}}{{\text{C}}_4}{{\text{H}}_9}{\text{OH(l)}} + {\text{C}}{{\text{r}}_2}{\text{O}}_7^{2 - }{\text{(aq)}} + {\text{8}}{{\text{H}}^ + }{\text{(aq)}} \to {\text{3}}{{\text{C}}_4}{{\text{H}}_8}{\text{O(l)}} + {\text{2C}}{{\text{r}}^{3 + }}{\text{(aq)}} + {\text{7}}{{\text{H}}_2}{\text{O(l)}}\);
Ignore state symbols.
(iii) \({\text{C}}{{\text{H}}_3}{\text{C}}{{\text{H}}_2}{\text{C}}{{\text{H}}_2}{\text{C}}{{\text{H}}_2}{\text{OH}}\);
\({{\text{(C}}{{\text{H}}_3}{\text{)}}_2}{\text{CHC}}{{\text{H}}_2}{\text{OH}}\);
Accept full or condensed structural formulas.
(iv) \({{\text{(C}}{{\text{H}}_3}{\text{)}}_3}{\text{COH}}\);
2-methylpropan-2-ol;
Allow 2-methyl-2-propanol, methylpropan-2-ol, methyl-2-propanol.
tertiary;
(v) \({{\text{C}}_4}{{\text{H}}_9}{\text{OH}} + {\text{6}}{{\text{O}}_2} \to {\text{4C}}{{\text{O}}_2} + {\text{5}}{{\text{H}}_2}{\text{O}}/{{\text{(C}}{{\text{H}}_3}{\text{)}}_3}{\text{COH}} + {\text{6}}{{\text{O}}_2} \to {\text{4C}}{{\text{O}}_2} + {\text{5}}{{\text{H}}_2}{\text{O}}\)
correct reactants and products;
correct balancing;
(i) \({\text{Z}} < {\text{W}} < {\text{X}} < {\text{Y}}\);
Accept Y > X > W > Z.
(ii) \({\text{X(s)}} + {{\text{Z}}^{2 + }}{\text{(aq)}} \to {{\text{X}}^{2 + }}{\text{(aq)}} + {\text{Z(s)}}\);
Ignore state symbols.
Accept X(s) + ZCl2(aq) \( \to \) XCl2(aq) + Z(s).
(iii) \({{\text{H}}_{\text{2}}}{\text{(g)}}\)/hydrogen;
(iv) diagram showing gas, solution and solid electrode;
For example,

This diagram scores [3].
\({\text{1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ }}{{\text{H}}^ + }{\text{(aq)}}\) and Pt;
Allow 1 mol L–1 or 1 M.
Allow 1 mol dm–3 HCl (aq) or other source of 1mol dm–3 H+(aq) ions.
100 kPa/\({\text{1}}{{\text{0}}^{\text{5}}}{\text{ Pa}}\)/1 bar (\({{\text{H}}_2}{\text{(g)}}\) pressure) and 298K / 25 °C;
Ignore state symbols throughout.
Allow 1.01 \( \times \) 105 Pa/1 atm.
(i) Positive electrode (anode):
\({{\text{I}}^ - }{\text{(aq)}} \to \frac{1}{2}{{\text{I}}_2}{\text{(aq)}} + {{\text{e}}^ - }\);
Accept correct equation involving 2 mols of I–.
Negative electrode (cathode):
\({{\text{H}}_2}{\text{O(l)}} + {{\text{e}}^ - } \to \frac{1}{2}{{\text{H}}_2}{\text{(g)}} + {\text{O}}{{\text{H}}^ - }{\text{(aq)}}/{{\text{H}}^ + }{\text{(aq)}} + {{\text{e}}^ - } \to \frac{1}{2}{{\text{H}}_2}{\text{(g)}}/\)
\({{\text{H}}_3}{{\text{O}}^ + }{\text{(aq)}} + {{\text{e}}^ - } \to {{\text{H}}_2}{\text{O(l)}} + \frac{1}{2}{{\text{H}}_2}{\text{(g)}}\);
Award [1 max] if correct equations are given at the wrong electrodes.
Ignore state symbols.
Allow e instead of e–.
Penalize equilibrium sign once only.
Accept correct equation involving 2 mols of H+.
(ii) aluminium will be oxidized (instead of \({{\text{I}}^ - }\)) at positive electrode (anode);
aluminium is a reactive metal / oxidation of aluminium has a positive \({E^\Theta }\) /
aluminium is higher on the reactivity series than \({{\text{I}}^ - }\) / OWTTE;
(i) \({{\text{n}}_{{\text{Sn}}}} = {{\text{n}}_{{\text{Cu}}}} = 2.86 \times {10^{ - 4}}/0.000286{\text{ (mol)}}\);
\({\text{m(Cu)}} = 2.86 \times {10^{ - 4}} \times 63.55 = 0.0182{\text{ (g)}}\);
(ii) blue colour persists in second cell and fades in third cell;
pH does not change in second cell and decreases in third cell;
Award [1 max] if both colour and pH are correctly stated for one only of either second or third cell.
(iii) Colour:
positive Cu electrode (anode) is oxidized to maintain colour in second cell / \({\text{Cu(s)}} \to {\text{C}}{{\text{u}}^{2 + }}{\text{(aq)}} + {\text{2}}{{\text{e}}^ - }\);
pH:
in third cell, \({{\text{H}}^ + }\) ions are produced as water is oxidized at positive electrode (anode) / \({{\text{H}}_2}{\text{O(l)}} \to \frac{1}{2}{{\text{O}}_2}{\text{(g)}} + {\text{2}}{{\text{H}}^ + }{\text{(aq)}} + {\text{2}}{{\text{e}}^ - }\) / solution becomes acidic as hydroxide ions are oxidized at positive electrode (anode) / \({\text{2O}}{{\text{H}}^ - }{\text{(aq)}} \to \frac{1}{2}{{\text{O}}_2}{\text{(g)}} + {{\text{H}}_2}{\text{O(l)}} + {\text{2}}{{\text{e}}^ - }\);
Ignore state symbols.
Examiners report
Most candidates attempted writing half reactions, but few got them correct in a(i), a(ii), b(ii), c(i) and d(iii). The structure and conditions for the standard hydrogen electrode produced a range of marks, and there was a significant minority who drew two half cells. The importance of the nature of the electrodes was hardly ever explained, if comments about the inert nature of aluminium due to its oxide coating were mentioned they would have been given credit. Once again the inability to describe and then explain the processes happening during the electrolysis of copper sulphate was apparent.
Most candidates attempted writing half reactions, but few got them correct in a(i), a(ii), b(ii), c(i) and d(iii). The structure and conditions for the standard hydrogen electrode produced a range of marks, and there was a significant minority who drew two half cells. The importance of the nature of the electrodes was hardly ever explained, if comments about the inert nature of aluminium due to its oxide coating were mentioned they would have been given credit. Once again the inability to describe and then explain the processes happening during the electrolysis of copper sulphate was apparent.
Most candidates attempted writing half reactions, but few got them correct in a(i), a(ii), b(ii), c(i) and d(iii). The structure and conditions for the standard hydrogen electrode produced a range of marks, and there was a significant minority who drew two half cells. The importance of the nature of the electrodes was hardly ever explained, if comments about the inert nature of aluminium due to its oxide coating were mentioned they would have been given credit. Once again the inability to describe and then explain the processes happening during the electrolysis of copper sulphate was apparent.
Most candidates attempted writing half reactions, but few got them correct in a(i), a(ii), b(ii), c(i) and d(iii). The structure and conditions for the standard hydrogen electrode produced a range of marks, and there was a significant minority who drew two half cells. The importance of the nature of the electrodes was hardly ever explained, if comments about the inert nature of aluminium due to its oxide coating were mentioned they would have been given credit. Once again the inability to describe and then explain the processes happening during the electrolysis of copper sulphate was apparent.
Acids can be described as strong or weak.
(i) Outline the difference in dissociation between strong and weak acids of the same concentration.
(ii) Describe three tests that can be carried out in the laboratory, and the expected results, to distinguish between \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ HCl(aq)}}\) and \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ C}}{{\text{H}}_{\text{3}}}{\text{COOH(aq)}}\).
Calculate the pH, using table 15 of the data booklet, of a solution of ethanoic acid made by dissolving 1.40 g of the acid in distilled water to make a \({\text{500 c}}{{\text{m}}^{\text{3}}}\) solution.
Determine the pH at the equivalence point of the titration and the \({\text{p}}{K_{\text{a}}}\) of an unknown acid using the acid-base titration curve below.

Identify, using table 16 of the data booklet, a suitable indicator to show the end-point of this titration.
Describe how an indicator, that is a weak acid, works. Use Le Chatelier’s principle in your answer.
State the formula of the conjugate base of chloroethanoic acid, \({\text{C}}{{\text{H}}_{\text{2}}}{\text{ClCOOH}}\).
Identify, with a reason, whether chloroethanoic acid is weaker or stronger than ethanoic acid using table 15 of the data booklet.
Determine the pH of the solution resulting when \({\text{100 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.50 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) \({\text{C}}{{\text{H}}_{\text{2}}}{\text{ClCOOH}}\) is mixed with \({\text{200 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) NaOH.
Describe how chlorine’s position in the periodic table is related to its electron arrangement.
\({\text{SC}}{{\text{l}}_{\text{2}}}\) and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) are two sulfur chloride type compounds with sulfur having different oxidation states. Predict the name of the shape, the bond angle and polarity of these molecules.
Markscheme
(i) weak acids dissociate only partially and strong acids (are assumed to) dissociate fully;
(ii) measuring electrical conductivity and strong acids have greater electrical conductivity/weak acids have lower electrical conductivity;
Do not accept conductivity for electrical conductivity.
Accept explanation in terms of lightbulb in circuit.
measure pH/use universal indicator and pH higher for weak acid/pH lower for strong acid;
conduct titration with a strong base and equivalence point higher for weak acid / buffer region for weak acid;
adding a reactive metal/carbonate/hydrogen carbonate and stronger effervescence/faster reaction with strong acids;
Accept converse argument.
Accept correct example.
adding a strong base and strong acid would increase more in temperature/weak acids increase less in temperature;
Accept correct example.
Award [1 max] for three suitable tests without correct results.
Accept specific examples with given strong acid and weak acid.
Accept “addition of \(AgN{O_3}(aq)\) and white precipitate with HCl (aq)”.
Do not accept “smell”.
\(\frac{{1.40}}{{60.06}} = 0.0233{\text{ (mol)}}\,\,\,\)and\(\,\,\,\frac{{0.0233}}{{0.500}} = 0.0466{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}})\);
\({\text{(p}}{K_{\text{a}}} = 4.76{\text{)}}{K_{\text{a}}} = 1.7 \times {10^{ - 5}}\);
\({\text{[}}{{\text{H}}^ + }{\text{]}} = \sqrt {{K_{\text{a}}}{\text{[HA]}}} = 8.9 \times {10^{ - 4}}\);
Accept \(9.0 \times 1{0^{ - {\text{4}}}}\).
\({\text{pH}} = 3.05\);
Award [4] for correct final answer.
Accept alternative methods.
Equivalence point: pH of 9.5;
Accept values between 9 and 10.
\({\text{p}}{K_{\text{a}}} = {\text{pH}}\) at half equivalence point;
\({\text{p}}{K_{\text{a}}} = 5.4\);
Accept any value between 5.2 and 5.6.
Award [2] for M2 and M3 if correct \(p{K_a}\) given without explanation.
phenolphthalein;
\({\text{HIn(aq)}} \rightleftharpoons {{\text{H}}^ + }{\text{(aq)}} + {\text{I}}{{\text{n}}^ - }{\text{(aq)}}\) and HIn and \({\text{I}}{{\text{n}}^ - }\) have different colours;
Ignore state symbols.
equilibrium shifts depending on addition of \({{\text{H}}^ + }\) and \({\text{O}}{{\text{H}}^ - }\) / more HIn in acid/low pH / more \({\text{I}}{{\text{n}}^ - }\) in alkali/high pH;
\({\text{C}}{{\text{H}}_{\text{2}}}{\text{ClCO}}{{\text{O}}^ - }\);
stronger because \({\text{p}}{K_{\text{a}}}\) of chloroethanoic acid is \( < {\text{p}}{K_{\text{a}}}\) of ethanoic acid;
Concentration of acid: \(\frac{{0.030}}{{0.300}} = 0.10{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
Concentration of base/salt: \(\frac{{0.020}}{{0.300}} = 0.067{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\([{{\text{H}}^ + }] = \frac{{{K_{\text{a}}} \times [{\text{HA}}]}}{{[{{\text{A}}^ - }]}}/\frac{{1.3 \times {{10}^{ - 3}} \times 0.10}}{{0.067}}{\text{/}}1.9 \times {10^{ - 3}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({\text{pH}} = 2.72\);
Award [4] for correct final answer.
Accept 2.69, 2.70 or 2.7.
Alternative for M3 and M4 if Henderson-Hasselbalch equation used:
M3: \(pH = p{K_a} + log\frac{{[base]}}{{[acid]}}{\text{/ }}2.87 + log\left( {\frac{{{\text{0.067}}}}{{0.10}}} \right)\)
M4: \(pH = 2.70\).
Award [1 max] for \({n_{acid}} ( = 100 \times 0.50 \div 1000) = 0.050 mol\) and
\({n_{base}}( = 200 \times 0.10 \div 1000) = 0.020 mol\).
Cl has 7 valence electrons and is in group 7;
Accept “group 17” as suggested by IUPAC.
Cl has 3 occupied (electron) shells/energy levels and so is in period 3;
Do not accept ECF for bond angles and polarities from incorrect shapes.
Award [3] for all six correct.
Award [2] for four or five correct.
Award [1] for two or three correct.
Examiners report
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
This question is about the compounds of some period 3 elements.
State the equations for the reactions of sodium oxide with water and phosphorus(V) oxide with water.
Explain why the melting point of phosphorus(V) oxide is lower than that of sodium oxide in terms of their bonding and structure.
Predict whether phosphorus(V) oxide and sodium oxide conduct electricity in their solid and molten states. Complete the boxes with “yes” or “no”.

Predict and explain the pH of the following aqueous solutions, using equations to support your answer.
Ammonium chloride, \({\text{N}}{{\text{H}}_{\text{4}}}{\text{Cl(aq)}}\):
Sodium methanoate, \({\text{HCOONa(aq)}}\):
Markscheme
\({\text{N}}{{\text{a}}_{\text{2}}}{\text{O(s)}} + {{\text{H}}_{\text{2}}}{\text{O(l)}} \to {\text{2NaOH(aq);}}\)
Accept \(N{a_2}O(s) + {H_2}O(l) \to 2N{a^ + }(aq) + 2O{H^ - }(aq)\).
\({{\text{P}}_4}{{\text{O}}_{10}}{\text{(s)}} + {\text{6}}{{\text{H}}_2}{\text{O(l)}} \to {\text{4}}{{\text{H}}_3}{\text{P}}{{\text{O}}_4}{\text{(aq)}}\);
Accept \({P_2}{O_5}(s) + 3{H_2}O(l) \to 2{H_3}P{O_4}(aq)\).
Accept \({P_4}{O_{10}}(s) + 6{H_2}O(l) \to 4{H^ + }(aq) + 4{H_2}PO_4^ - (aq)\).
Ignore state symbols.
\({\text{N}}{{\text{a}}_{\text{2}}}{\text{O}}\) ionic and \({{\text{P}}_{\text{4}}}{{\text{O}}_{{\text{10}}}}\) covalent (within molecule);
\({\text{N}}{{\text{a}}_{\text{2}}}{\text{O}}\) in giant/3D/network/lattice structure with strong (ionic) bonds and \({{\text{P}}_{\text{4}}}{{\text{O}}_{{\text{10}}}}\) has a (simple) molecular structure/weak intermolecular forces (between molecules);
Award [1] for stating that bonds require more energy to break in \(N{a_2}O\) than in \({P_4}{O_{10}}\).
 ;
;
Award [2] for four correct.
Award [1] for two or three correct.
Ammonium chloride:
Accept any value in the range: \(3 < {\text{pH}} < 7\);
\({\text{NH}}_4^ + {\text{(aq)}} \rightleftharpoons {\text{N}}{{\text{H}}_3}{\text{(aq)}} + {{\text{H}}^ + }{\text{(aq)}}\);
Sodium methanoate:
\(7 < {\text{pH}} < 11\);
\({\text{HCO}}{{\text{O}}^ - }{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{HCOOH(aq)}} + {\text{O}}{{\text{H}}^ - }{\text{(aq)}}\);
Award [1 max] for both M1 and M3 combined if stated “pH < 7/acidic for ammonium chloride and pH > 7/alkaline/basic for sodium methanoate”.
Accept alternative suitable equations.
Award [1 max] for two correct explanations, such as “salt of weak acid and strong base” or “salt of weak base and strong acid”, without equations.
Penalize missing equilibrium sign once only.
Ignore state symbols.
Examiners report
In (a) sodium oxide was answered better than phosphorus(V) oxide (a direct reference to Assessment Statement 13.1.1) although there were many instances of NaO. In (b) there were the usual suggestions that covalent bonds are weaker than ionic bonds. Candidates find the distinction between inter- and intra-molecular bonding very difficult to grasp. Some didn’t realize that \({\text{N}}{{\text{a}}_{\text{2}}}{\text{O}}\) is ionic. Answers about electrical conductivity usually gained one of the two marks available so there may have been an element of guesswork here. Many answers to (c) gained only one mark for knowing that one would be acidic and the other basic. There was very poor understanding of the equations needed and the explanation of the equilibria involved.
In (a) sodium oxide was answered better than phosphorus(V) oxide (a direct reference to Assessment Statement 13.1.1) although there were many instances of NaO. In (b) there were the usual suggestions that covalent bonds are weaker than ionic bonds. Candidates find the distinction between inter- and intra-molecular bonding very difficult to grasp. Some didn’t realize that \({\text{N}}{{\text{a}}_{\text{2}}}{\text{O}}\) is ionic. Answers about electrical conductivity usually gained one of the two marks available so there may have been an element of guesswork here. Many answers to (c) gained only one mark for knowing that one would be acidic and the other basic. There was very poor understanding of the equations needed and the explanation of the equilibria involved.
In (a) sodium oxide was answered better than phosphorus(V) oxide (a direct reference to Assessment Statement 13.1.1) although there were many instances of NaO. In (b) there were the usual suggestions that covalent bonds are weaker than ionic bonds. Candidates find the distinction between inter- and intra-molecular bonding very difficult to grasp. Some didn’t realize that \({\text{N}}{{\text{a}}_{\text{2}}}{\text{O}}\) is ionic. Answers about electrical conductivity usually gained one of the two marks available so there may have been an element of guesswork here. Many answers to (c) gained only one mark for knowing that one would be acidic and the other basic. There was very poor understanding of the equations needed and the explanation of the equilibria involved.
In (a) sodium oxide was answered better than phosphorus(V) oxide (a direct reference to Assessment Statement 13.1.1) although there were many instances of NaO. In (b) there were the usual suggestions that covalent bonds are weaker than ionic bonds. Candidates find the distinction between inter- and intra-molecular bonding very difficult to grasp. Some didn’t realize that \({\text{N}}{{\text{a}}_{\text{2}}}{\text{O}}\) is ionic. Answers about electrical conductivity usually gained one of the two marks available so there may have been an element of guesswork here. Many answers to (c) gained only one mark for knowing that one would be acidic and the other basic. There was very poor understanding of the equations needed and the explanation of the equilibria involved.
Consider the following list of organic compounds.
Compound 1: \({\text{C}}{{\text{H}}_{\text{3}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{CH(OH)C}}{{\text{H}}_{\text{3}}}\)
Compound 2: \({\text{C}}{{\text{H}}_{\text{3}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{COC}}{{\text{H}}_{\text{3}}}\)
Compound 3: \({\text{C}}{{\text{H}}_{\text{3}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{OH}}\)
Compound 4: \({\text{C}}{{\text{H}}_{\text{3}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{CHO}}\)
Apply IUPAC rules to state the names of the four compounds.
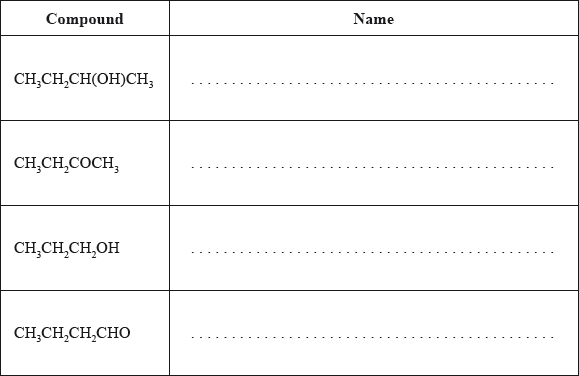
(i) Define the term structural isomers.
(ii) Identify the two compounds in the list that are structural isomers of each other.
(i) Determine the organic product formed when each of the compounds is heated under reflux with excess acidified potassium dichromate(VI). If no reaction occurs write NO REACTION in the table.
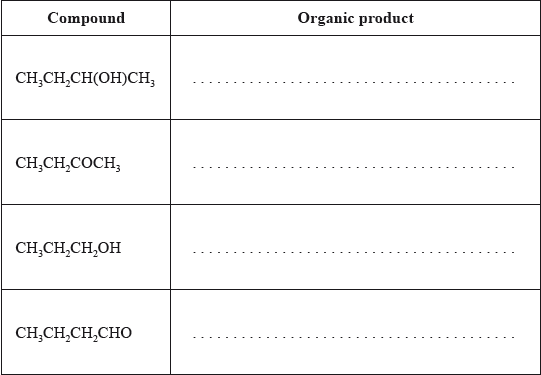
(ii) Describe the colour change during the reactions that occur in part (i).
(i) Pentanoic acid reacts with ethanol. State the structural formula of the organic product and the name of the functional group it contains.
(ii) State the type of reaction in part (i).
Describe what is meant by a weak Brønsted-Lowry base, including an equation for the reaction of ammonia with water.
Markscheme
(i) same molecular formula but differ in arrangement of their atoms;
Allow “different structures/structural formulas” instead of “different arrangement of atoms”.
(ii) (compounds) 2 and 4 / butanone and butanal;
(i) 
(ii) orange to green;
(i) \({\text{C}}{{\text{H}}_{\text{3}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{COOC}}{{\text{H}}_{\text{2}}}{\text{C}}{{\text{H}}_{\text{3}}}\);
ester;
(ii) condensation / addition-elimination;
Accept esterification.
a base is a proton acceptor;
weak means it is only partially ionized/dissociated (in solution/water);
\({\text{N}}{{\text{H}}_3} + {{\text{H}}_2}{\text{O}} \rightleftharpoons {\text{NH}}_4^ + + {\text{O}}{{\text{H}}^ - }{\text{ }}\);
Reversible arrow is required for M3.
Examiners report
The naming of the organic compounds was generally well answered, though quite frequently candidates benefited from the decision not to penalise the unnecessary “2” in “butan-2-one”. Propanol was a frequent incorrect answer.
(i) Generally well answered but there were some answers that reflected a poor understanding of structural isomerism.
(ii) Well answered.
(i) Generally well answered. But some candidates gave propanal as the product for propan-1-ol, and other candidates were confused about the products of the oxidation of alcohols.
(ii) Most candidates knew the colour change of the dichromate solution during the reaction.
(i) Most candidates identified and drew the ester correctly.
(ii) Very well answered.
About half of the candidates gained full marks. Many candidates omitted the reversible arrow. Some candidates only answered part of the question.
Bleaches in which chlorine is the active ingredient are the most common, although some environmental groups have concerns about their use.
In aqueous chlorine the equilibrium below produces chloric(I) acid (hypochlorous acid), HOCl, the active bleach.
\[{\text{C}}{{\text{l}}_2}{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{HOCl(aq)}} + {{\text{H}}^ + }{\text{(aq)}} + {\text{C}}{{\text{l}}^ - }{\text{(aq)}}\]
Aqueous sodium chlorate(I), NaOCl, the most common active ingredient in chlorine based bleaches, oxidizes coloured materials to colourless products while being reduced to the chloride ion. It will also oxidize sulfur dioxide to the sulfate ion.
The standard electrode potential for the reduction of the chlorate(V) ion to the chloride ion is \( + 1.49{\text{ V}}\).
(i) Describe the colour change that occurs when aqueous chlorine is added to aqueous sodium bromide.
(ii) Outline, with the help of a chemical equation, why this reaction occurs.
Chloric(I) acid is a weak acid, but hydrochloric acid is a strong acid. Outline how this is indicated in the equation above.
State a balanced equation for the reaction of chloric(I) acid with water.
Outline, in terms of the equilibrium in aqueous chlorine, why it is dangerous to use an acidic toilet cleaner in combination with this kind of bleach.
Suggest why a covalent molecule, such as chloric(I) acid, is readily soluble in water.
Partial neutralization of chloric(I) acid creates a buffer solution. Given that the \({\text{p}}{K_{\text{a}}}\) of chloric(I) acid is 7.53, determine the pH of a solution that has \({\text{[HOCl]}} = 0.100{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) and \({\text{[Cl}}{{\text{O}}^ - }{\text{]}} = 0.0500{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\).
Describe, using HIn to represent the indicator in its acid form, why an indicator changes colour when excess alkali is added.
(i) Deduce a balanced equation for the reaction between the chlorate(I) ion and sulfur dioxide from the appropriate half-equations.
(ii) State the initial and final oxidation numbers of both chlorine and sulfur in the final equation.

(i) Define the term standard electrode potential.
(ii) Referring to Table 14 of the Data Booklet, deduce, giving a reason, whether the oxidation of the chromium(III) ion to the dichromate(VI) ion by the chlorate(V) ion is energetically feasible.
Markscheme
(i) from (pale) green/colourless to yellow/orange/brown;
Initial colour must be stated.
Do not accept “clear/transparent” instead of “colourless”.
(ii) chlorine more reactive/more powerful oxidizing agent (than bromine);
Accept opposite statements for bromine.
Accept “chloride ion a weaker reducing agent” / “bromide ion a stronger reducing agent”.
Accept “chlorine more electronegative than bromine”.
\({\text{C}}{{\text{l}}_2}{\text{(aq)}} + {\text{2NaBr(aq)}} \to {\text{B}}{{\text{r}}_2}{\text{(aq)}} + {\text{2NaCl(aq)}}/{\text{C}}{{\text{l}}_2}{\text{(aq)}} + {\text{2B}}{{\text{r}}^ - }{\text{(aq)}} \to {\text{B}}{{\text{r}}_2}{\text{(aq)}} + {\text{2C}}{{\text{l}}^ - }{\text{(aq)}}\);
Ignore state symbols.
Do not accept with equilibrium sign.
chloric(I) acid (shown as) a molecule/molecular, but hydrochloric acid (shown as being) split into ions / OWTTE;
Accept “chloric(I) acid is partially dissociated and hydrochloric acid is fully dissociated”.
Reference needed to both acids for mark.
\({\text{HOCl(aq)}} \rightleftharpoons {{\text{H}}^ + }{\text{(aq)}} + {\text{Cl}}{{\text{O}}^ - }{\text{(aq)}}/{\text{HOCl(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {{\text{H}}_3}{{\text{O}}^ + }{\text{(aq)}} + {\text{Cl}}{{\text{O}}^ - }{\text{(aq)}}\);
Equilibrium sign required for the mark.
Ignore state symbols.
acid displaces the equilibrium to the left (to form chlorine);
chlorine is toxic/poisonous/harmful/lung irritant;
Accept answers that refer to the (b) (ii) equilibrium.
chloric(I) acid has –OH group / hydrogen attached to a very electronegative atom;
Accept polar molecule.
can form hydrogen bonds to water;
hydrogen bonding to water increases its solubility;
(as a weak acid it is) in equilibrium with ions;
\({K_{\text{a}}} = {10^{ - 7.53}} = 2.95 \times {10^{ - 8}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}})\);
\({K_{\text{a}}} = \frac{{{\text{[}}{{\text{H}}^ + }{\text{][Cl}}{{\text{O}}^ - }{\text{]}}}}{{{\text{[HOCl]}}}} = \frac{{{\text{[}}{{\text{H}}^ + }{\text{](0.05)}}}}{{{\text{(0.1)}}}} \approx \frac{{{\text{[}}{{\text{H}}^ + }{\text{]}}}}{2} = {\text{2.95}} \times {\text{1}}{{\text{0}}^{ - 8}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({\text{[}}{{\text{H}}^ + }{\text{]}} = 2 \times 2.95 \times {10^{ - 8}} = 5.9 \times {10^{ - 8}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({\text{pH}} = - \log (5.9 \times {10^{ - 8}}) = 7.23\);
Accept other methods of carrying out the calculation.
Award [4] for correct final answer.
\({\text{HIn}} \rightleftharpoons {{\text{H}}^ + } + {\text{I}}{{\text{n}}^ - }\);
Do not accept equation without equilibrium arrow.
(weak acid in which the) acid/HIn and conjugate base/In– have different colours / OWTTE;
excess alkali shifts the equilibrium to the RHS/towards the conjugate base;
(i) \({\text{Cl}}{{\text{O}}^ - }{\text{(aq)}} + {\text{2}}{{\text{H}}^ + }{\text{(aq)}} + {\text{2}}{{\text{e}}^ - } \rightleftharpoons {{\text{H}}_2}{\text{O(l)}} + {\text{C}}{{\text{l}}^ - }{\text{(aq)}}\);
\({\text{SO}}_4^{2 - }{\text{(aq)}} + {\text{4}}{{\text{H}}^ + }{\text{(aq)}} + {\text{2}}{{\text{e}}^ - } \rightleftharpoons {\text{S}}{{\text{O}}_2}{\text{(aq)}} + {\text{2}}{{\text{H}}_2}{\text{O(l)}}\);
Accept SO42–(aq) + 4H+(aq) + 2e– \( \rightleftharpoons \) H2SO3(aq) + H2O(l).
For final equation:
\({\text{Cl}}{{\text{O}}^ - }{\text{(aq)}} + {\text{S}}{{\text{O}}_2}{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{SO}}_4^{2 - }{\text{(aq)}} + {\text{2}}{{\text{H}}^ + }{\text{(aq)}} + {\text{C}}{{\text{l}}^ - }{\text{(aq)}}\)
Accept ClO–(aq) + H2SO3(aq) \( \rightleftharpoons \) SO42–(aq) + 2H+(aq) + Cl–(aq).
correct reactants and products;
balancing and cancelling \({{\text{e}}^ - }\), \({{\text{H}}^ + }\) and \({{\text{H}}_2}{\text{O}}\);
Apply ECF if incorrect half-equations written.
Ignore state symbols and absence of equilibrium arrow for all equations and accept inclusion of Na+ in any equation.
(ii) Award [2] for all correct, [1] for 2 or 3 correct.

Remember to apply ECF from final (c) (i) equation.
Penalise incorrect notation (eg, 4 or 4+ rather than +4) once only, so award [1] for a fully correct answer in an incorrect format.
(i) potential (of reduction half-reaction) under standard conditions measured
relative to standard hydrogen electrode/SHE / OWTTE;
Allow “solute concentration of 1 mol dm–3” or “1 bar/1 atm (pressure) for gases” instead of “standard conditions”.
(ii) yes / energetically feasible;
would have a positive \({E_{{\text{cell}}}}\) / chlorate(V) ion stronger oxidizing agent than dichromate(VI) ion / OWTTE;
Examiners report
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Soluble acids and bases ionize in water.
A solution containing 0.510 g of an unknown monoprotic acid, HA, was titrated with 0.100 mol dm–3 NaOH(aq). 25.0 cm3 was required to reach the equivalence point.
The following curve was obtained using a pH probe.
State, giving a reason, the strength of the acid.
State a technique other than a pH titration that can be used to detect the equivalence point.
Deduce the pKa for this acid.
The pKa of an anthocyanin is 4.35. Determine the pH of a 1.60 × 10–3 mol dm–3 solution to two decimal places.
Markscheme
weak AND pH at equivalence greater than 7
OR
weak acid AND forms a buffer region
[1 mark]
calorimetry
OR
measurement of heat/temperature
OR
conductivity measurement
Accept “indicator” but not “universal indicator”.
[1 mark]
«pKa = pH at half-equivalence =» 5.0
[1 mark]
Ka = \({10^{ - 4.35}}/4.46683 \times {10^{ - 5}}\)
[H3O+] = \(\sqrt {4.46683 \times {{10}^{ - 5}} \times 1.60 \times {{10}^{ - 3}}} \,\,\,/\,\,\sqrt {7.1469 \times {{10}^{ - 8}}} \,\,/\,\,2.6734 \times {10^{ - 4}}\) «mol dm–3»
pH = «\( - \log \sqrt {7.1469 \times {{10}^{ - 8}}} = \)» 3.57
Award [3] for correct final answer to two decimal places.
If quadratic equation used, then: [H3O+] = 2.459 × 10–4 «mol dm–3» and pH = 3.61
[3 marks]
Examiners report
Two chemistry students wished to determine the enthalpy of hydration of anhydrous magnesium sulfate. They measured the initial and the highest temperature reached when anhydrous magnesium sulfate, \({\text{MgS}}{{\text{O}}_{\text{4}}}{\text{(s)}}\), was dissolved in water. They presented their results in the table below.

The students repeated the experiment using 6.16 g of solid hydrated magnesium sulfate, \({\text{MgS}}{{\text{O}}_{\text{4}}} \bullet {\text{7}}{{\text{H}}_{\text{2}}}{\text{O(s)}}\), and \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of water. They found the enthalpy change, \(\Delta {H_2}\) , to be \( + {\text{18 kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\).
The enthalpy of hydration of solid anhydrous magnesium sulfate is difficult to determine experimentally, but can be determined using the diagram below.
(i) Calculate the amount, in mol, of anhydrous magnesium sulfate.
(ii) Calculate the enthalpy change, \(\Delta {H_1}\), for anhydrous magnesium sulfate dissolving in water, in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\). State your answer to the correct number of significant figures.
(i) Determine the enthalpy change, \(\Delta H\), in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\), for the hydration of solid anhydrous magnesium sulfate, \({\text{MgS}}{{\text{O}}_{\text{4}}}\).
(ii) The literature value for the enthalpy of hydration of anhydrous magnesium sulfate is \( - 103{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\). Calculate the percentage difference between the literature value and the value determined from experimental results, giving your answer to one decimal place. (If you did not obtain an answer for the experimental value in (b)(i) then use the value of \( - 100{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\), but this is not the correct value.)
Another group of students experimentally determined an enthalpy of hydration of \( - 95{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\). Outline two reasons which may explain the variation between the experimental and literature values.
Magnesium sulfate is one of the products formed when acid rain reacts with dolomitic limestone. This limestone is a mixture of magnesium carbonate and calcium carbonate.
(i) State the equation for the reaction of sulfuric acid with magnesium carbonate.
(ii) Deduce the Lewis (electron dot) structure of the carbonate ion, giving the shape and the oxygen-carbon-oxygen bond angle.
Lewis (electron dot) structure:
Shape:
Bond angle:
(iii) There are three possible Lewis structures that can be drawn for the carbonate ion, which lead to a resonance structure. Explain, with reference to the electrons, why all carbon-oxygen bonds have the same length.
(iv) Deduce the hybridization of the carbon atom in the carbonate ion.
Markscheme
(i) \(n{\text{(MgS}}{{\text{O}}_4}{\text{)}} = \left( {\frac{{3.01}}{{120.37}} = } \right)0.0250{\text{ (mol)}}\);
(ii) energy released \( = 50.0 \times 4.18 \times 9.7 \times 2027{\text{ (J)}}/2.027{\text{ (kJ)}}\);
\(\Delta {H_1} = - 81{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
Award [2] for correct answer.
Award [2] if 53.01 is used giving an answer of –86 (kJ mol–1).
Award [1 max] for +81/81/+86/86 (kJ mol−1).
Award [1 max] for –81000/–86000 if units are stated as J mol−1.
Allow answers to 3 significant figures.
(i) \(\Delta H{\text{ (}} = \Delta {H_1} - \Delta {H_2}{\text{)}} = - 99{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
Award [1] if –86 is used giving an answer of –104 (kJ mol–1).
(ii) \(\frac{{(103 - 99)}}{{103}} \times 100 = 3.9\% \);
Accept answer of 2.9% if –100 used but only if a value for (b)(i) is not present.
Award [1] if –104 is used giving an answer of 1.0% .
Accept correct answers which are not to 1 decimal place.
\({\text{MgS}}{{\text{O}}_{\text{4}}}\) not completely anhydrous / OWTTE;
\({\text{MgS}}{{\text{O}}_{\text{4}}}\) is impure;
heat loss to the atmosphere/surroundings;
specific heat capacity of solution is taken as that of pure water;
experiment was done once only so it is not scientific;
density of solution is taken to be \({\text{1 g}}\,{\text{c}}{{\text{m}}^{ - 3}}\);
mass of \({\text{7}}{{\text{H}}_2}{\text{O}}\) ignored in calculation;
uncertainty of thermometer is high so temperature change is unreliable;
literature values determined under standard conditions, but this experiment is not;
all solid not dissolved;
(i) \({{\text{H}}_2}{\text{S}}{{\text{O}}_4}{\text{(aq)}} + {\text{MgC}}{{\text{O}}_3}{\text{(s)}} \to {\text{MgS}}{{\text{O}}_4}{\text{(aq)}} + {\text{C}}{{\text{O}}_2}{\text{(g)}} + {{\text{H}}_2}{\text{O(l)}}\);
Ignore state symbols.
Do not accept H2CO3.
(ii) 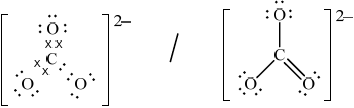 ;
;
Accept crosses, lines or dots as electron pairs.
Accept any correct resonance structure.
Award [0] if structure is drawn without brackets and charge.
Award [0] if lone pairs not shown on O atoms.
shape: trigonal/triangular planar;
bond angle: 120° ;
Accept answers trigonal/triangular planar and 120° if M1 incorrect, but no other answers should be given credit.
(iii) (pi/\(\pi \)) electrons are delocalized/spread over more than two nuclei / charge spread (equally) over all three oxygens;
(iv) \({\text{s}}{{\text{p}}^{\text{2}}}\);
Examiners report
The use of 3.01 for the mass in the expression in \(Q = mc\Delta T\) was common, candidates were able to score in the subsequent parts and many did so, although there was often a confusion between the value Q and the required answer for \(\Delta H\). In part c) most candidates understood the error due to heat loss, but few scored the second mark, usually quoting an answer involving an error generally that was far too vague. The inability to construct a balanced equation was disappointing, many lost credit for giving \({{\text{H}}_{\text{2}}}{\text{C}}{{\text{O}}_{\text{3}}}\) as a product. The score for the structure of the carbonate ion was often lost due to the failure to show that a charge is present on the ion, however, the shape and bond angle were known well, as was delocalisation and hybridisation.
The use of 3.01 for the mass in the expression in \(Q = mc\Delta T\) was common, candidates were able to score in the subsequent parts and many did so, although there was often a confusion between the value Q and the required answer for \(\Delta H\). In part c) most candidates understood the error due to heat loss, but few scored the second mark, usually quoting an answer involving an error generally that was far too vague. The inability to construct a balanced equation was disappointing, many lost credit for giving \({{\text{H}}_{\text{2}}}{\text{C}}{{\text{O}}_{\text{3}}}\) as a product. The score for the structure of the carbonate ion was often lost due to the failure to show that a charge is present on the ion, however, the shape and bond angle were known well, as was delocalisation and hybridisation.
The use of 3.01 for the mass in the expression in \(Q = mc\Delta T\) was common, candidates were able to score in the subsequent parts and many did so, although there was often a confusion between the value Q and the required answer for \(\Delta H\). In part c) most candidates understood the error due to heat loss, but few scored the second mark, usually quoting an answer involving an error generally that was far too vague. The inability to construct a balanced equation was disappointing, many lost credit for giving \({{\text{H}}_{\text{2}}}{\text{C}}{{\text{O}}_{\text{3}}}\) as a product. The score for the structure of the carbonate ion was often lost due to the failure to show that a charge is present on the ion, however, the shape and bond angle were known well, as was delocalisation and hybridisation.
The use of 3.01 for the mass in the expression in \(Q = mc\Delta T\) was common, candidates were able to score in the subsequent parts and many did so, although there was often a confusion between the value Q and the required answer for \(\Delta H\). In part c) most candidates understood the error due to heat loss, but few scored the second mark, usually quoting an answer involving an error generally that was far too vague. The inability to construct a balanced equation was disappointing, many lost credit for giving \({{\text{H}}_{\text{2}}}{\text{C}}{{\text{O}}_{\text{3}}}\) as a product. The score for the structure of the carbonate ion was often lost due to the failure to show that a charge is present on the ion, however, the shape and bond angle were known well, as was delocalisation and hybridisation.
Nitrogen monoxide reacts at 1280 °C with hydrogen to form nitrogen and water. All reactants and products are in the gaseous phase.
The gas-phase decomposition of dinitrogen monoxide is considered to occur in two steps.
\[\begin{array}{*{20}{l}} {{\text{Step 1:}}}&{{{\text{N}}_2}{\text{O(g)}}\xrightarrow{{{k_1}}}{{\text{N}}_2}({\text{g)}} + {\text{O(g)}}} \\ {{\text{Step 2:}}}&{{{\text{N}}_2}{\text{O(g)}} + {\text{O(g)}}\xrightarrow{{{k_2}}}{{\text{N}}_2}({\text{g)}} + {{\text{O}}_2}{\text{(g)}}} \end{array}\]
The experimental rate expression for this reaction is rate \( = k{\text{[}}{{\text{N}}_2}{\text{O]}}\).
The conversion of \({\text{C}}{{\text{H}}_{\text{3}}}{\text{NC}}\) into \({\text{C}}{{\text{H}}_{\text{3}}}{\text{CN}}\) is an exothermic reaction which can be represented as follows.
\({\text{C}}{{\text{H}}_{\text{3}}}–{\text{N}}\)\( \equiv \)\({\text{C}} \to {\text{transition state}} \to {\text{C}}{{\text{H}}_{\text{3}}}–{\text{C}}\)\( \equiv \)\({\text{N}}\)
This reaction was carried out at different temperatures and a value of the rate constant, \(k\), was obtained for each temperature. A graph of \(\ln k\) against \(1/T\) is shown below.
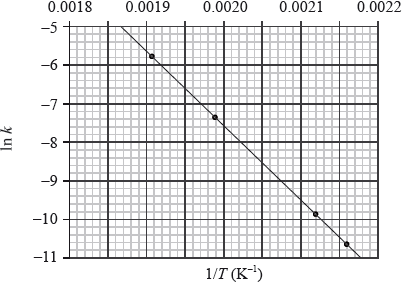
Define the term rate of reaction.
State an equation for the reaction of magnesium carbonate with dilute hydrochloric acid.
The rate of this reaction in (a) (ii), can be studied by measuring the volume of gas collected over a period of time. Sketch a graph which shows how the volume of gas collected changes with time.
The experiment is repeated using a sample of hydrochloric acid with double the volume, but half the concentration of the original acid. Draw a second line on the graph you sketched in part (a) (iii) to show the results in this experiment. Explain why this line is different from the original line.
The kinetics of the reaction were studied at this temperature. The table shows the initial rate of reaction for different concentrations of each reactant.
Deduce the order of the reaction with respect to NO and \({{\text{H}}_2}\), and explain your reasoning.
Deduce the rate expression for the reaction.
Determine the value of the rate constant for the reaction from Experiment 3 and state its units.
Identify the rate-determining step.
Identify the intermediate involved in the reaction.
Define the term activation energy, \({E_{\text{a}}}\).
Construct the enthalpy level diagram and label the activation energy, \({E_{\text{a}}}\), the enthalpy change, \(\Delta H\), and the position of the transition state.
Describe qualitatively the relationship between the rate constant, \(k\), and the temperature, \(T\).
Calculate the activation energy, \({E_{\text{a}}}\), for the reaction, using Table 1 of the Data Booklet.
Markscheme
decrease in concentration/mass/amount/volume of reactant with time / increase in concentration/mass/amount/volume of product with time / change in concentration/mass/amount/volume of reactant/product with time;
\({\text{MgC}}{{\text{O}}_3}{\text{(s)}} + {\text{2HCl(aq)}} \to {\text{MgC}}{{\text{l}}_2}{\text{(aq)}} + {\text{C}}{{\text{O}}_2}{\text{(g)}} + {{\text{H}}_2}{\text{O(l)}}\);
Ignore state symbols.
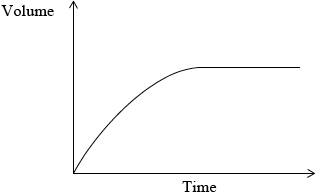 ;
;
Plot starts at the origin and levels off.
No mark awarded if axes are not labelled.
new curve reaches same height as original curve;
new curve less steep than original curve;
volume of gas produced is the same because the same amount of acid is used;
reaction is slower because concentration is decreased;
(from experiments 1 and 2 at constant \({\text{[}}{{\text{H}}_2}{\text{]}}\)), [NO] doubles, rate quadruples;
hence, second order with respect to NO;
(from experiments 2 and 3 at constant [NO]), \({\text{[}}{{\text{H}}_{\text{2}}}{\text{]}}\)doubles, rate doubles;
first order with respect to \({{\text{H}}_2}\);
Allow alternative mathematical deductions also.
\({\text{rate}} = k{{\text{[NO]}}^{\text{2}}}{\text{[}}{{\text{H}}_{\text{2}}}{\text{]}}\);
\(k\left( { = (10.00 \times {{10}^{ - 5}})/{{(10.00 \times {{10}^{ - 3}})}^2}(4.00 \times {{10}^{ - 3}})} \right) = 2.50 \times {10^2}\);
Do not penalize if Experiments 1 or 2 are used to determine k.
\({\text{mo}}{{\text{l}}^{ - 2}}{\text{d}}{{\text{m}}^6}{{\text{s}}^{ - 1}}\);
step 1 / equation showing step 1;
O (atom) / oxygen atom;
Do not allow oxygen or O2.
(minimum) energy needed for a reaction to occur / difference in energy between the reactants and transition state;

correct position of activation energy;
correct position of \(\Delta H\) and \(H{\text{(C}}{{\text{H}}_3}{\text{NC)}}\)/reactant line above \(H{\text{(C}}{{\text{H}}_3}{\text{CN)}}\) product line;
Accept \(\Delta E\) instead of \(\Delta H\) on diagram if y-axis is labelled as energy.
Do not penalize if CH3NC and CH3CN are not labelled on diagram.
correct position of transition state;
Allow [2 max] if axes are not labelled on diagram.
as temperature/\(T\) increases rate constant/k increases (exponentially);
from graph gradient \(m = - \frac{{{E_{\text{a}}}}}{R}\);
measurement of gradient from chosen points on graph;
Units of m are K. Do not penalize if not given, but do not award mark for incorrect units.
Value of m is based on any two suitable points well separated on the plot.
correct answer for \({E_{\text{a}}}\);
correct units corresponding to answer;
Note: A typical answer for Ea = 1.6 \( \times \) 102 kJ / kJ\(\,\)mol–1.
Examiners report
Surprisingly, the rate of reaction was only correctly defined by approximately 50% of candidates in (a) (i).
The equation for the reaction of magnesium carbonate with dilute hydrochloric acid was not well answered (part (ii)), and often candidates did not write correct formula or forgot to include water as a product.
Part (iii) was well answered by most candidates.
Part (iv) was well answered by most candidates, although the weaker candidates often only scored two or three marks.
Part (b) (i) was well answered and many candidates scored all four marks. Some candidates used a simple mathematical approach and those that followed this method typically were able to deduce the order correctly.
For (ii) most candidates were able to write the rate expression for the reaction.
In (iii), determining the value of the rate constant and its corresponding units was difficult for many candidates and only the better candidates scored both marks. Many mistakes were seen in the units.
Part (c) (i) was usually well answered.
A common mistake for (ii) involved candidates writing \({{\text{O}}_{\text{2}}}\) instead of O.
The definition of activation energy was well answered.
Part (ii) was a question where most candidates scored at least one/two marks although perfect answers were less common. Reasons leading to the loss of marks included: absence of axes, incomplete libelling of axes and the incorrect identification of the position of the transition state.
Parts (iii) and (iv) were very poorly answered for such a fundamental topic. All sorts of errors were evident, including incorrect gradients, inability to rearrange the Arrhenius Equation etc.
Even the better candidates struggled greatly with this question, even though this comes straight from AS 16.3.2.
When nitrogen gas and hydrogen gas are allowed to react in a closed container the following equilibrium is established.
\[{{\text{N}}_{\text{2}}}{\text{(g)}} + {\text{3}}{{\text{H}}_{\text{2}}}{\text{(g)}} \rightleftharpoons {\text{2N}}{{\text{H}}_{\text{3}}}{\text{(g) }}\Delta H = -92.6{\text{ kJ}}\]
Outline two characteristics of a reversible reaction in a state of dynamic equilibrium.
Predict, with a reason, how each of the following changes affects the position of equilibrium.
The volume of the container is increased.
Ammonia is removed from the equilibrium mixture.
Define the term activation energy, \({E_{\text{a}}}\).
Ammonia is manufactured by the Haber process in which iron is used as a catalyst.
Explain the effect of a catalyst on the rate of reaction.
Typical conditions used in the Haber process are 500 °C and 200 atm, resulting in approximately 15% yield of ammonia.
(i) Explain why a temperature lower than 500 °C is not used.
(ii) Outline why a pressure higher than 200 atm is not often used.
Deduce the equilibrium constant expression, \({K_{\text{c}}}\), for the reaction on page 10.
When 1.00 mol of nitrogen and 3.00 mol of hydrogen were allowed to reach equilibrium in a \({\text{1.00 d}}{{\text{m}}^{\text{3}}}\) container at a temperature of 500 °C and a pressure of 1000 atm, the equilibrium mixture contained 1.46 mol of ammonia.
Calculate the value of \({K_{\text{c}}}\) at 500 °C.
Define the term base according to the Lewis theory.
Define the term weak base according to the Brønsted–Lowry theory.
Deduce the formulas of conjugate acid-base pairs in the reaction below.
\[{\text{C}}{{\text{H}}_{\text{3}}}{\text{N}}{{\text{H}}_{\text{2}}}{\text{(aq)}} + {{\text{H}}_{\text{2}}}{\text{O(l)}} \rightleftharpoons {\text{C}}{{\text{H}}_{\text{3}}}{\text{NH}}_{\text{3}}^ + {\text{(aq)}} + {\text{O}}{{\text{H}}^ - }{\text{(aq)}}\]
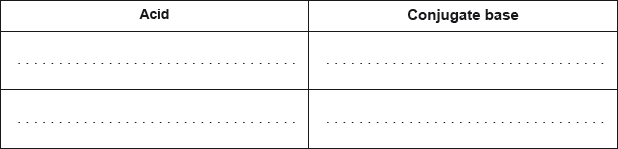
Determine the pH of a \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of ammonia, \({\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\), using tables 2 and 15 of the data booklet.
(i) Sketch the pH titration curve obtained when \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\) is added to \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{HCl (aq)}}\).
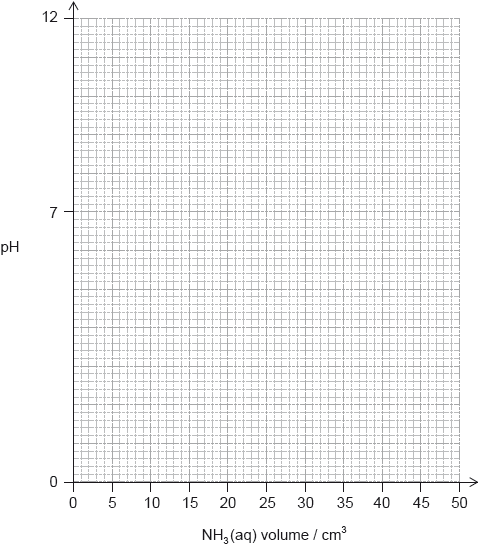
(ii) Identify an indicator from table 16 of the data booklet that could be used for this titration.
Markscheme
rates of forward and reverse reactions are equal / opposing changes occur at equal rates;
the concentrations of all reactants and products remain constant / macroscopic properties remain constant;
closed/isolated system;
Accept “the same” for “equal” in M1 and for “constant” in M2.
The volume of the container is increased:
position of equilibrium shifts to the left/reactants and fewer moles of gas on the right hand side/pressure decreases / OWTTE;
Ammonia is removed from the equilibrium mixture:
position of equilibrium shifts to the right/products and \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) decreases so \({\text{[}}{{\text{N}}_{\text{2}}}{\text{]}}\) and \({\text{[}}{{\text{H}}_{\text{2}}}{\text{]}}\) must also decrease to keep Kc constant
OR
position of equilibrium shifts to the right/products and rate of reverse reaction decreases / OWTTE;
Award [1 max] if both predicted changes are correct.
Do not accept “to increase \([N{H_3}]\)” or reference to LCP without explanation.
minimum energy needed (by reactants/colliding particles) to react/start/initiate a reaction;
Accept “energy difference between reactants and transition state”.
more effective/successful collisions per unit time / greater proportion of collisions effective;
alternative pathway and a lower activation energy
OR
lowers activation energy so that more particles have enough energy to react;
Do not accept just “lowers/reduces the activation energy”.
Accept “provides a surface for reacting/reactants/reaction”.
(i) slower rate / OWTTE;
uneconomic / OWTTE;
(ii) high cost for building/maintaining plant / high energy cost of compressor / OWTTE;
Do not accept “high pressure is expensive” without justification.
Accept high pressure requires high energy.
\(({K_{\text{c}}} = )\frac{{{{{\text{[N}}{{\text{H}}_3}{\text{(g)]}}}^2}}}{{{\text{[}}{{\text{N}}_2}{\text{(g)]}} \times {{{\text{[}}{{\text{H}}_2}{\text{(g)]}}}^3}}}\);
Ignore state symbols.
Concentrations must be represented by square brackets.
moles at equilibrium: nitrogen 0.27, hydrogen 0.81 / concentrations at equilibrium: nitrogen \({\text{0.27 (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\), hydrogen \({\text{0.81 (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) (and ammonia \({\text{1.46 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\));
\({K_{\text{c}}} = 15\);
Actual calculation gives \({K_{\text{c}}}{\text{ = }}14{\text{.}}86\).
Award [2] for correct final answer.
Award [1 max] if \({K_{\text{c}}}\left( { = \frac{{{{1.46}^2}}}{{{3^3} \times 1}}} \right) = 0.079\)
electron pair donor;
Accept lone pair donor.
proton acceptor and partially/slightly ionized;
Accept “proton acceptor and partially/slightly dissociated”.
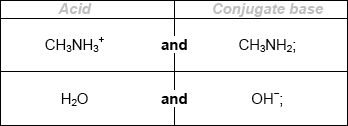
Award [1 max] for two correct acids OR two correct conjugate bases.
\({K_{\text{b}}} = \frac{{{\text{[NH}}_4^ + {\text{][O}}{{\text{H}}^ - }{\text{]}}}}{{{\text{[N}}{{\text{H}}_3}{\text{]}}}} = 1.8 \times {10^{ - 5}}/{10^{ - 4.75}}\);
\({\text{[NH}}_4^ + {\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\) and \({\text{[N}}{{\text{H}}_3}{\text{]}} \approx 1.00 \times {10^{ - 1}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({\text{[O}}{{\text{H}}^ - }{\text{]}} = (\sqrt {1.8 \times {{10}^{ - 6}}} = )1.3 \times {10^{ - 3}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}/{\text{pOH}} = 2.89\);
\({\text{pH}} = (14.0 - 2.89 = )11.1\);
Award [4] for correct final answer.
(i) 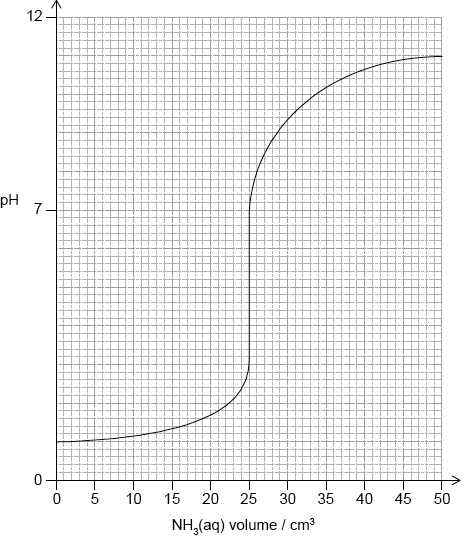
For volume \( = 0:{\text{ pH}} = 1\);
vertical jump should be positioned in volume range \({\text{24 c}}{{\text{m}}^{\text{3}}}\) to \({\text{26 c}}{{\text{m}}^{\text{3}}}\) and include pH range between 3 to 6;
For volume = 50: pH between 8 to 11;
(ii) methyl orange / bromophenol blue / bromocresol green / methyl red;
Examiners report
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
Most candidates were able to give two characteristics of a dynamic equilibrium and explain the effect of changes in volume on the position of equilibrium but many had difficulty giving a complete explanation of the equilibrium shift resulting from the removal of ammonia. Candidates were expected to include a reference to the value of \({K_{\text{c}}}\) or the reduced rate of the reverse reaction when justifying their answer. The definition of activation energy was well known but some lost a mark in their explanation of catalyst action as they did not refer to an alternative pathway in their explanation for the lower activation energy. The explanation of why lower temperatures were not used in the Haber process was also incomplete with many not considering the economic disadvantages of a slow reaction rate. Similarly many did not explain why high pressure was expensive in terms of energy or building costs. Most were able to deduce the equilibrium constant but many lost a mark in the calculation of \({K_{\text{c}}}\) as they used the initial concentrations of nitrogen and hydrogen. Some teachers identified an inconsistency in the question in that the total number of moles of gas under the conditions stated in the question was not consistent with the ideal gas equation however this did not appear to be a problem for the candidates. (However, the ideal gas law cannot be applied here as under these conditions ammonia would be in its supercritical state.) Most candidates were able to define Lewis bases but the definition of weak Brønsted-Lowry bases proved to be more problematic as many did not refer to partial ionisation in their response. Most students were able to identify the conjugate acid-base pairs. The calculation of the pH of an ammonia solution proved to be challenging with many confusing \({K_{\text{a}}}\) and \({K_{\text{b}}}\). Others did not recognize that since it is a weak base, \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) at equilibrium is approximately equal to starting concentration \({\text{(0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\) or that \({\text{[NH}}{{\text{4}}^ + }{\text{]}} = {\text{[O}}{{\text{H}}^ - }{\text{]}}\). (The examination paper was rescaled for candidates sitting the examination in Spanish (due to the error in the question) and candidates close to a boundary given particular attention.) Only the strongest candidates were able to gain full marks for the pH curve although many recognised that the pH would be 1 before any ammonia was added given that HCl is a strong acid. A significant number had the final pH above 11 and did not allow for dilution of the \({\text{0.1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution. Many correctly identified a possible indicator.
\({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.200 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ethanoic acid was added to \({\text{30.0 c}}{{\text{m}}^{\text{3}}}\) of a \({\text{0.150 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydrogencarbonate solution, \({\text{NaHC}}{{\text{O}}_{\text{3}}}{\text{(aq)}}\).
The molar mass of a volatile organic liquid, X, can be determined experimentally by allowing it to vaporize completely at a controlled temperature and pressure. 0.348 g of X was injected into a gas syringe maintained at a temperature of 90 °C and a pressure of \(1.01 \times {10^5}{\text{ Pa}}\). Once it had reached equilibrium, the gas volume was measured as \({\text{95.0 c}}{{\text{m}}^{\text{3}}}\).
Bromoethane, \({\text{C}}{{\text{H}}_{\text{3}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{Br}}\), undergoes a substitution reaction to form ethylamine, \({\text{C}}{{\text{H}}_{\text{3}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{N}}{{\text{H}}_{\text{2}}}\).
Many organic compounds exist as stereoisomers.
Outline how electrical conductivity can be used to distinguish between a \({\text{0.200 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of ethanoic acid, \({\text{C}}{{\text{H}}_{\text{3}}}{\text{COOH}}\), and a \({\text{0.200 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of hydrochloric acid, HCl.
(i) State an equation for the reaction of ethanoic acid with a solution of sodium hydrogencarbonate.
(ii) Determine which is the limiting reagent. Show your working.
(iii) Calculate the mass, in g, of carbon dioxide gas produced.
(i) Determine the amount, in mol, of X in the gas syringe.
(ii) Calculate the molar mass of X.
Deduce the mechanism for the reaction using equations and curly arrows to represent the movement of electron pairs.
(i) Outline the meaning of the term stereoisomers.
(ii) Draw the structures of the two stereoisomers of dichloroethene, \({{\text{C}}_{\text{2}}}{{\text{H}}_{\text{2}}}{\text{C}}{{\text{l}}_{\text{2}}}\).
(iii) Explain why this type of stereoisomerism exists in \({{\text{C}}_{\text{2}}}{{\text{H}}_{\text{2}}}{\text{C}}{{\text{l}}_{\text{2}}}\).
(iv) Draw the structures of the two stereoisomers of 1-chloro-1-fluoroethane, \({{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{FCl}}\), showing the relationship between them.
(v) Outline how the two isomers of \({{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{FCl}}\) could be distinguished from each other.
Markscheme
HCl is a strong acid and \({\text{C}}{{\text{H}}_3}{\text{COOH}}\) is a weak acid so HCl has higher conductivity / HCl dissociates completely in water and \({\text{C}}{{\text{H}}_3}{\text{COOH}}\) does not, so HCl has higher conductivity / HCl is a stronger acid (than \({\text{C}}{{\text{H}}_{\text{3}}}{\text{COOH}}\)) so has higher \({\text{[}}{{\text{H}}^ + }{\text{]}}\) and higher conductivity;
(i) \({\text{C}}{{\text{H}}_3}{\text{COOH(aq)}} + {\text{HCO}}_3^ - {\text{(aq)}} \to {\text{C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ - }{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} + {\text{C}}{{\text{O}}_2}{\text{(g)}}\);
Accept NaHCO3(aq) and CH3COONa (aq) instead of ions.
Ignore state symbols.
(ii) \(n({\text{C}}{{\text{H}}_3}{\text{COOH}}) = 0.00500{\text{ (mol)}}\) and \(n{\text{(NaHC}}{{\text{O}}_3}{\text{)}} = 0.00450{\text{ (mol)}}\);
\({\text{NaHC}}{{\text{O}}_3}\) is limiting;
(iii) \(n{\text{(C}}{{\text{O}}_2}{\text{)}} = n{\text{(NaHC}}{{\text{O}}_{\text{3}}}{\text{)}} = 0.00450{\text{ (mol)}}\);
\(m{\text{(C}}{{\text{O}}_2}{\text{)}} = 0.00450 \times 44.01 = 0.198{\text{(g)}}\);
Award [2] for correct final answer.
(i) \(T = 363{\text{ K}}\) and \(V = 9.50 \times {10^{ - 5}}{\text{ }}{{\text{m}}^3}\);
Accept V = 9.5 \( \times \) 10–2 dm3 if P is used as 101 kPa in calculation.
\(n = \frac{{PV}}{{RT}} = \frac{{1.01 \times {{10}^5} \times 9.50 \times {{10}^{ - 5}}}}{{8.31 \times 363}}\);
\( = 3.18 \times {10^{ - 3}}{\text{ (mol)}}\);
Award [3] for correct final answer.
(ii) \(M - \left( {\frac{m}{n} = \frac{{0.348}}{{3.18 \times {{10}^{ - 3}}}} = } \right){\text{ }}109{\text{ (g}}\,{\text{mo}}{{\text{l}}^{ - {\text{1}}}}{\text{)}}\);

curly arrow going from lone pair on N in \({\text{N}}{{\text{H}}_{\text{3}}}\) to C;
curly arrow showing Br leaving;
Accept curly arrow going from bond between C and Br to Br on 1-bromoethane or on the transition state.
representation of transition state showing square brackets, two partial bonds and curly arrow going from NH bond to NC partial bond/curly arrow going from NH bond to N;
Do not penalize if NH3 and Br are not at 180° to each other.
Do not award M3 if NH3—C bond is represented.
(i) compounds with same structural formula but different arrangements of atoms in space;
(ii)
The two structures must be clear 3D representations of mirror images.
Tapered (wedge/dash) notation not necessary.
(iii) restricted rotation around (C=C) double bond;
(iv)
(v) the two enantiomers rotate the plane of plane-polarized light by equal amounts, but in opposite directions;
using a polarimeter;
Examiners report
Poorly constructed symbolic equations on what should be relatively simple reactions once again impeded candidates from credit. The use of \(pV = nRT\) often scored for error carried forward even when they lost the first mark from incorrect use of units for pressure. The attempts at the \({{\text{S}}_{\text{N}}}{\text{2}}\) mechanisms were generally poor, with errors both in the attacking nucleophile, and the sloppy use of curly arrows which indicate that many students have a basic lack of understanding about what they represent. While candidates could score the first two marks, the third mark was almost never awarded. Conditions and reagents in d(ii) and d(iii) were rarely known, and definitions of stereoisomers and the representation of 3D structures was disappointing.
Poorly constructed symbolic equations on what should be relatively simple reactions once again impeded candidates from credit. The use of \(pV = nRT\) often scored for error carried forward even when they lost the first mark from incorrect use of units for pressure. The attempts at the \({{\text{S}}_{\text{N}}}{\text{2}}\) mechanisms were generally poor, with errors both in the attacking nucleophile, and the sloppy use of curly arrows which indicate that many students have a basic lack of understanding about what they represent. While candidates could score the first two marks, the third mark was almost never awarded. Conditions and reagents in d(ii) and d(iii) were rarely known, and definitions of stereoisomers and the representation of 3D structures was disappointing.
Poorly constructed symbolic equations on what should be relatively simple reactions once again impeded candidates from credit. The use of \(pV = nRT\) often scored for error carried forward even when they lost the first mark from incorrect use of units for pressure. The attempts at the \({{\text{S}}_{\text{N}}}{\text{2}}\) mechanisms were generally poor, with errors both in the attacking nucleophile, and the sloppy use of curly arrows which indicate that many students have a basic lack of understanding about what they represent. While candidates could score the first two marks, the third mark was almost never awarded. Conditions and reagents in d(ii) and d(iii) were rarely known, and definitions of stereoisomers and the representation of 3D structures was disappointing.
Poorly constructed symbolic equations on what should be relatively simple reactions once again impeded candidates from credit. The use of \(pV = nRT\) often scored for error carried forward even when they lost the first mark from incorrect use of units for pressure. The attempts at the \({{\text{S}}_{\text{N}}}{\text{2}}\) mechanisms were generally poor, with errors both in the attacking nucleophile, and the sloppy use of curly arrows which indicate that many students have a basic lack of understanding about what they represent. While candidates could score the first two marks, the third mark was almost never awarded. Conditions and reagents in d(ii) and d(iii) were rarely known, and definitions of stereoisomers and the representation of 3D structures was disappointing.
Poorly constructed symbolic equations on what should be relatively simple reactions once again impeded candidates from credit. The use of \(pV = nRT\) often scored for error carried forward even when they lost the first mark from incorrect use of units for pressure. The attempts at the \({{\text{S}}_{\text{N}}}{\text{2}}\) mechanisms were generally poor, with errors both in the attacking nucleophile, and the sloppy use of curly arrows which indicate that many students have a basic lack of understanding about what they represent. While candidates could score the first two marks, the third mark was almost never awarded. Conditions and reagents in d(ii) and d(iii) were rarely known, and definitions of stereoisomers and the representation of 3D structures was disappointing.
A voltaic cell was set up, using the standard hydrogen electrode as a reference electrode and a standard \({\text{C}}{{\text{u}}^{2 + }}{\text{(aq)/Cu(s)}}\) electrode.
Another voltaic cell was set up, using a \({\text{S}}{{\text{n}}^{2 + }}{\text{(aq)/Sn(s)}}\) half-cell and a \({\text{C}}{{\text{u}}^{2 + }}{\text{(aq)/Cu(s)}}\) half-cell under standard conditions.
Water in a beaker at a pressure of \(1.01 \times {10^5}{\text{ Pa}}\) and a temperature of 298 K will not spontaneously decompose. However, decomposition of water can be induced by means of electrolysis.
Define oxidation in terms of oxidation number.
Deduce the balanced chemical equation for the redox reaction of copper, Cu(s), with nitrate ions, \({\text{N}}{{\text{O}}^{3 - }}{\text{(aq)}}\), in acid, to produce copper(II) ions, \({\text{C}}{{\text{u}}^{2 + }}{\text{(aq)}}\), and nitrogen(IV) oxide, \({\text{N}}{{\text{O}}_{\text{2}}}{\text{(g)}}\).
Deduce the oxidizing and reducing agents in this reaction.
Oxidizing agent:
Reducing agent:
Describe the standard hydrogen electrode including a fully labelled diagram.
Define the term standard electrode potential, \({E^\Theta }\).
Deduce a balanced chemical equation, including state symbols, for the overall reaction which will occur spontaneously when the two half-cells are connected.
Draw a fully labelled diagram of the voltaic cell, showing the positive electrode (cathode), the negative electrode (anode) and the direction of electron movement through the external circuit.
Using Table 14 of the Data Booklet, calculate the cell potential, \(E_{{\text{cell}}}^\Theta \), in V, when the two half-cells are connected.
Deduce the sign of the standard free energy change, \(\Delta {G^\Theta }\), for any non-spontaneous reaction.
State why dilute sulfuric acid needs to be added in order for the current to flow in the electrolytic cell.
State why copper electrodes cannot be used in the electrolysis of water. Suggest instead suitable metallic electrodes for this electrolysis process.
Deduce the half-equations for the reactions occurring at the positive electrode (anode) and the negative electrode (cathode).
Positive electrode (anode):
Negative electrode (cathode):
Deduce the overall cell reaction, including state symbols.
Draw a fully labelled diagram of the electrolytic cell, showing the positive electrode (anode) and the negative electrode (cathode).
Comment on what is observed at both electrodes.
Two electrolytic cells are connected in series (the same current passes through each cell). One cell for the electrolysis of water produces 100 cm\(^3\) of oxygen, measured at 273 K and \(1.01 \times {10^5}{\text{ Pa}}\). The second cell contains molten lead(II) bromide, \({\text{PbB}}{{\text{r}}_{\text{2}}}\). Determine the mass, in g, of lead produced.
Markscheme
increase (in oxidation number);
\({\text{Cu(s)}} + {\text{2NO}}_3^ - {\text{(aq)}} + {\text{4}}{{\text{H}}^ + }{\text{(aq)}} \to {\text{C}}{{\text{u}}^{2 + }}{\text{(aq)}} + {\text{2N}}{{\text{O}}_2}{\text{(g)}} + {\text{2}}{{\text{H}}_2}{\text{O(l) /}}\)
\({\text{Cu(s)}} + {\text{2HN}}{{\text{O}}_3}{\text{(aq)}} + {\text{2}}{{\text{H}}^ + }{\text{(aq)}} \to {\text{C}}{{\text{u}}^{2 + }} + {\text{2N}}{{\text{O}}_2}{\text{(g)}} + {\text{2HO(l)}}\);
correct reactants and products;
fully balanced chemical equation;
Ignore state symbols.
M1 can be scored if there are unbalanced electrons in equation.
M2 can only be scored if M1 is correct.
M2 can be scored if there are balanced electrons on both sides of equation.
Oxidizing agent: \({\text{NO}}_{\text{3}}^ - \)/nitrate/\({\text{HN}}{{\text{O}}_{\text{3}}}\)/nitric acid and Reducing agent: Cu/copper;
Diagram showing gas, solution and solid electrode;
For example,
\({\text{1 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ }}{{\text{H}}^ + }\) (aq) and Pt;
Allow 1 mol L–1 or 1 M.
Allow 1 mol dm–3 HCl (aq) or other source of 1mol dm−3 H+(aq) ions.
100 kPa/10\(^5\) Pa/1 bar (H\(_2\) (g) pressure) and 298K / 25 °C;
Ignore state symbols throughout.
Allow 1.01×10\(^5\) Pa/1 atm.
potential of reduction half-reaction under standard conditions measured relative to standard hydrogen electrode/SHE / potential under standard conditions relative to standard hydrogen electrode/SHE;
Instead of standard conditions allow either solute concentration of 1 mol\(\,\)dm–3 or 100 kPa/105 Pa/1 bar (pressure) for gases (allow 1 atm).
Allow voltage/EMF instead of potential.
\({\text{C}}{{\text{u}}^{2 + }}{\text{(aq)}} + {{\text{H}}_2}{\text{(g)}} \to {\text{Cu(s)}} + {\text{2}}{{\text{H}}^ + }{\text{(aq)}}\)
reactants and products;
fully balanced chemical equation, including state symbols;
M2 cannot be scored if M1 is incorrect.
Voltaic cell showing:
Labelled positive electrode (cathode): Cu2+ /Cu and negative electrode (anode): Sn2+ /Sn;
Do not penalize if state symbols are not included (since given in question).
voltmeter and salt bridge;
Voltmeter can be labelled or drawn as a circle with a V.
Allow ammeter/A.
Salt bridge can be labelled, represented with drawing connecting the two half-cells, labelled as potassium nitrate or using its chemical formula (for example, KNO3) etc.
correct direction of electron movement from Sn to Cu in external circuit;
\(( + )0.48{\text{ (V)}}\);
positive;
provides ions (to carry current) / water poor conductor (of electricity);
Do not accept electrons instead of ions.
copper reacts so (nonreactive metal such as) Pt used;
Accept Ag, Au or any named metal less reactive than copper as electrode.
Do not accept Cu reacts with water or graphite as electrode.
Positive electrode (anode):
\({\text{2}}{{\text{H}}_2}{\text{O(l)}} \to {{\text{O}}_2}{\text{(g)}} + {\text{4}}{{\text{H}}^ + }{\text{(aq)}} + {\text{4}}{{\text{e}}^ - }{\text{ / 4O}}{{\text{H}}^ - }{\text{(aq)}} \to {{\text{O}}_2}{\text{(g)}} + {\text{2}}{{\text{H}}_2}{\text{O(l)}} + {\text{4}}{{\text{e}}^ - }\);
Negative electrode (cathode):
\({{\text{H}}^ + }{\text{(aq)}} + {{\text{e}}^ - } \to \frac{1}{2}{{\text{H}}_2}{\text{(g) / 4}}{{\text{H}}^ + }{\text{(aq)}} + {\text{4}}{{\text{e}}^ - } \to {\text{2}}{{\text{H}}_2}{\text{(g) / 2}}{{\text{H}}^ + }{\text{(aq)}} + {\text{2}}{{\text{e}}^ - } \to {{\text{H}}_2}{\text{ /}}\)
\({\text{2}}{{\text{H}}_2}{\text{O(l)}} + {\text{2}}{{\text{e}}^ - } \to {{\text{H}}_2}{\text{(g)}} + {\text{2O}}{{\text{H}}^ - }{\text{(aq) / }}{{\text{H}}_2}{\text{O(l)}} + {{\text{e}}^ - } \to \frac{1}{2}{{\text{H}}_2}{\text{(g)}} + {\text{O}}{{\text{H}}^ - }\);
Award [1 max] if M1 and M2 reversed.
Ignore state symbols.
Allow e instead of e–.
Do not penalize use of equilibrium sign instead of \( \to \).
Accept a multiple of the equations.
\({\text{2}}{{\text{H}}_2}{\text{O(l)}} \to {\text{2}}{{\text{H}}_2}{\text{(g)}} + {{\text{O}}_2}{\text{(g) / }}{{\text{H}}_2}{\text{O(l)}} \to {{\text{H}}_2}{\text{(g)}} + \frac{1}{2}{{\text{O}}_2}{\text{(g)}}\);
State symbols required as asked for in question.
Do not penalize use of equilibrium sign instead of \( \to \).
Do not accept any multiple of 2H+(aq) + 2OH–(aq) \( \to \) 2H2(g) + O2(g).
electrolytic cell showing solid electrodes immersed in solution;
positive electrode (anode) connected to positive terminal of battery and
negative electrode (cathode) to negative terminal;
Allow graphite or metal given in e(iii) as electrodes.
bubbles /gas produced;
Do not accept hydrogen is formed at cathode and oxygen formed at anode.
\(n({{\text{O}}_2}){\text{ }}\left( { = \left( {\frac{{100}}{{22.4 \times 1000}}} \right)} \right) = 4.46 \times {10^{ - 3}}{\text{ (mol)}}\);
\(m{\text{ }}\left( { = (4.46 \times {{10}^{ - 3}} \times 2 \times 207.19)} \right) = 1.85{\text{ (g)}}\);
OR
\(n({{\text{O}}_2}){\text{ }}\left( { = \frac{{{\text{PV}}}}{{{\text{RT}}}}} \right) = 4.45 \times {10^{ - 3}}{\text{ (mol)}}\);
\(m{\text{ }}( = 4.45 \times {10^{ - 3}} \times 2 \times 207.19) = 1.84{\text{ (g)}}\);
Examiners report
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Many made mistakes in writing a balanced equation for the reaction between Cu and HNO3, in drawing a diagram for a hydrogen electrode, in writing a definition of ‘standard electrode potential’. Most could draw a labeled diagram for an electrochemical cell. Many mistakes were made in writing balanced equations for reactions at the electrodes and overall equation for the electrolysis of water.
Phosphine (IUPAC name phosphane) is a hydride of phosphorus, with the formula PH3.
(i) Draw a Lewis (electron dot) structure of phosphine.
(ii) State the hybridization of the phosphorus atom in phosphine.
(iii) Deduce, giving your reason, whether phosphine would act as a Lewis acid, a Lewis base, or neither.
(iv) Outline whether you expect the bonds in phosphine to be polar or non-polar, giving a brief reason.
(v) Phosphine has a much greater molar mass than ammonia. Explain why phosphine has a significantly lower boiling point than ammonia.
(vi) Ammonia acts as a weak Brønsted–Lowry base when dissolved in water.
Outline what is meant by the terms “weak” and “Brønsted–Lowry base”.
Weak:
Brønsted–Lowry base:
Phosphine is usually prepared by heating white phosphorus, one of the allotropes of phosphorus, with concentrated aqueous sodium hydroxide. The equation for the reaction is:
(i) The first reagent is written as P4, not 4P. Describe the difference between P4 and 4P.
(ii) The ion H2PO2− is amphiprotic. Outline what is meant by amphiprotic, giving the formulas of both species it is converted to when it behaves in this manner.
(iii) State the oxidation state of phosphorus in P4 and H2PO2−.
P4:
H2PO2−:
(iv) Oxidation is now defined in terms of change of oxidation number. Explore how earlier definitions of oxidation and reduction may have led to conflicting answers for the conversion of P4 to H2PO2− and the way in which the use of oxidation numbers has resolved this.
2.478 g of white phosphorus was used to make phosphine according to the equation:
(i) Calculate the amount, in mol, of white phosphorus used.
(ii) This phosphorus was reacted with 100.0 cm3 of 5.00 mol dm−3 aqueous sodium hydroxide. Deduce, showing your working, which was the limiting reagent.
(iii) Determine the excess amount, in mol, of the other reagent.
(iv) Determine the volume of phosphine, measured in cm3 at standard temperature and pressure, that was produced.
Impurities cause phosphine to ignite spontaneously in air to form an oxide of phosphorus and water.
(i) 200.0 g of air was heated by the energy from the complete combustion of 1.00 mol phosphine. Calculate the temperature rise using section 1 of the data booklet and the data below.
Standard enthalpy of combustion of phosphine,
Specific heat capacity of air = 1.00Jg−1K−1=1.00kJkg−1K−1
(ii) The oxide formed in the reaction with air contains 43.6% phosphorus by mass. Determine the empirical formula of the oxide, showing your method.
(iii) The molar mass of the oxide is approximately 285 g mol−1. Determine the molecular formula of the oxide.
(iv) State the equation for the reaction of this oxide of phosphorus with water.
(v) Suggest why oxides of phosphorus are not major contributors to acid deposition.
(vi) The levels of sulfur dioxide, a major contributor to acid deposition, can be minimized by either pre-combustion and post-combustion methods. Outline one technique of each method.
Pre-combustion:
Post-combustion:
Markscheme
(i)
Accept structures using dots and/or crosses to indicate bonds and/or lone pair.
(ii)
sp3
Do not allow ECF from a (i).
(iii)
Lewis base AND has a lone pair of electrons «to donate»
(iv)
non-polar AND P and H have the same electronegativity
Accept “similar electronegativities”.
Accept “polar” if there is a reference to a small difference in electronegativity and apply ECF in 1 a (v).
(v)
PH3 has London «dispersion» forces
NH3 forms H-bonds
H-bonds are stronger
OR
London forces are weaker
Accept van der Waals’ forces, dispersion forces and instantaneous dipole – induced dipole forces.
Accept “dipole-dipole forces” as molecule is polar.
H-bonds in NH3 (only) must be mentioned to score [2].
Do not award M2 or M3 if:
• implies covalent bond is the H-bond
• implies covalent bonds break.
Accept “dipole-dipole forces are weaker”.
(vi)
Weak: only partially dissociated/ionized «in dilute aqueous solution»
Brønsted–Lowry base: an acceptor of protons/H+/hydrogen ions
Accept reaction with water is reversible/an equilibrium.
Accept “water is partially dissociated «by the weak base»”.
(i)
P4 is a molecule «comprising 4P atoms» AND 4P is four/separate «P» atoms
OR
P4 represents «4P» atoms bonded together AND 4P represents «4» separate/non-bonded «P» atoms
(ii)
can act as both a «Brønsted–Lowry» acid and a «Brønsted–Lowry» base
OR
can accept and/or donate a hydrogen ion/proton/H+
HPO22– AND H3PO2
(iii)
P4: 0
H2PO2–: +1
Do not accept 1 or 1+ for H2PO2−.
(iv)
oxygen gained, so could be oxidation
hydrogen gained, so could be reduction
OR
negative charge «on product/H2PO2 »/gain of electrons, so could be reduction
oxidation number increases so must be oxidation
Award [1 max] for M1 and M2 if candidate displays knowledge of at least two of these definitions but does not apply them to the reaction.
Do not award M3 for “oxidation number changes”.
(i)
«\(\left\langle {\frac{{2.478}}{{4 \times 30.97}}} \right\rangle \)»= 0.02000 «mol»
(ii)
n(NaOH) = «0.1000 × 5.00 =» 0.500 «mol» AND P4/phosphorus is limiting reagent
Accept n(H2O) = \(\frac{{100}}{{18}}\) = 5.50 AND P4 is limiting reagent.
(iii)
amount in excess «= 0.500 - (3 × 0.02000)» = 0.440 «mol»
(iv)
«22.7 × 1000 × 0.02000» = 454 «cm3»
Accept methods employing pV = nRT, with p as either 100 (454 cm3) or 101.3 kPa (448 cm3). Do not accept answers in dm3.
(i)
temperature rise «=\(\frac{{750 \times 1.00}}{{0.2000 \times 1.00}}\)»=3750«°C/K»
Do not accept −3750.
(ii)
n(P)«=\(\frac{{43.6}}{{30.97}}\)»=1.41 «mol»
n(O) «=\(\frac{{100 - 43.6}}{{16.00}}\)»=3.53 «mol»
«\(\frac{{n\left( {\rm{O}} \right)}}{{n\left( {\rm{P}} \right)}}\)=\(\frac{{3.53}}{{1.41}}\) = 2.50 so empirical formula is» P2O5
Accept other methods where the working is shown.
(iii)
«\(\frac{{285}}{{141.9}}\)=2.00, so molecular formula = 2×P2O5=»P4O10
(iv)
P4O10(s) + 6H2O (l) → 4H3PO4 (aq)
Accept P4O10(s) + 2H2O (l) → 4HPO3 (aq) (initial reaction)
Accept P2O5(s) + 3H2O(l) → 2H3PO4(aq)
Accept equations for P4O6/P2O3 if given in d (iii).
Accept any ionized form of the acids as the products.
(v)
phosphorus not commonly found in fuels
OR
no common pathways for phosphorus oxides to enter the air
OR
amount of phosphorus-containing organic matter undergoing anaerobic decomposition is small
Accept “phosphorus oxides are solids so are not easily distributed in the atmosphere”.
Accept “low levels of phosphorus oxide in the air”.
Do not accept “H3PO4 is a weak acid”.
(vi)
Pre-combustion:
remove sulfur/S/sulfur containing compounds
Post-combustion:
remove it/SO2 by neutralization/reaction with alkali/base
Accept “lime injection fluidised bed combustion” for either, but not both.
Examiners report
A student titrated two acids, hydrochloric acid, HCl (aq) and ethanoic acid, CH3COOH (aq), against 50.0 cm3 of 0.995 mol dm–3 sodium hydroxide, NaOH (aq), to determine their concentration. The temperature of the reaction mixture was measured after each acid addition and plotted against the volume of each acid.
Using the graph, estimate the initial temperature of the solutions.
Determine the maximum temperature reached in each experiment by analysing the graph.
Suggest why the enthalpy change of neutralization of CH3COOH is less negative than that of HCl.
Markscheme
21.4 °C
Accept values in the range of 21.2 to 21.6 °C.
Accept two different values for the two solutions from within range.
HCl: 30.4 «°C»
Accept range 30.2 to 30.6 °C.
CH3COOH: 29.0 «°C»
Accept range 28.8 to 29.2 °C.
CH3COOH is weak acid/partially ionised
energy used to ionize weak acid «before reaction with NaOH can occur»